How to find and use tangent or "tan" values to figure out the slope, pitch, rise, run of a ramp, road, roof, stair, or walkway.

How to use the tangent function to convert a pitch angle in degrees to inches of rise per foot of run.

This article series gives easy-to-understand examples of just about every possible way to figure out width, length, slope, rise, run, and unit rise in inches per foot of various structures, roads, walks, ramps, etc.

How to Use Tangents in Slope, Pitch or Rise Calculations

Article Contents

• DEFINE & USE TANGENTS for SLOPE or PITCH of ROOFS, STAIRS, WALKS
• CALCULATE the TAN VALUE from TWO SIDES of a TRIANGLE
• TANGENT CALCULATION or TANGENT TABLE
• TANGENT for a 12 in 12 SLOPE = Tan 45

[Click to enlarge any image]

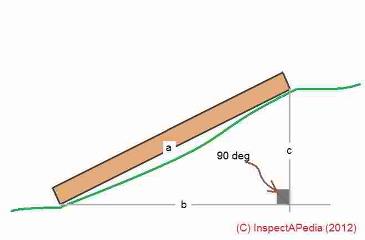
In our drawing just above the triangle's height is labled c and the length of the base labeled b and its hypotenuse is a.

Definition & Uses of Tangent & Tan^-1 when Working With a Right Triangle
(building roofs, stairs, walks, or whatever)

To be honest, in years of working as a carpenter and framer I don't recall making much use of the tan or tangent function to do my rafter or stair stringer calculations. But sometimes we are given data about the pitch or slope of a roof, stair, walk, road, etc. that needs to be converted to simple rise & run numbers before we can get to work.

That's where the tan or tangent function becomes very helpful. Don't be intimidated by geometry. And don't try looking up the definition of tangent or you'll feel even worse.

The following definition makes tangents useful to carpenters and other builders since we will often work with triangles such as the slope of a rafter over an attic floor or under a roof - our sketch above.

Definition of Tangent: the Tangent of any angle is defined as the vertical rise divided by the horizontal run.

A tangent is also defined as a ratio of two lengths: the length of the side of the triangle opposite the angle divided by the length of the adjacent side of the angle.

For a right triangle (such as a roofing triangle) in which the roof rise is the vertical line opposite the roof angle or slope, the tangent of the roof angle is the ratio of roof rise over the length of the sloped roof surface.

Or in geometry speak:

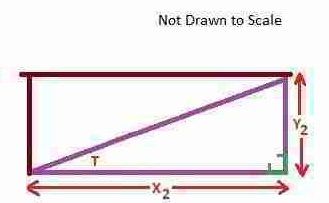
Height Y₁ / Length X₁ = Height Y₂ / Length X₂

as long as we keep the slope or angle unchanged.

The tangent function is simply a ratio of horizontal run X and vertical rise Y.

For any stairway of a given angle or slope (say 38 degrees in your case) the ratio of run (x) to rise (y) will remain the same.

That's why once you set your stair slope (too steeply) at 38 degrees, we can calculate the rise or run for any stair tread dimension (tread depth or run or tread height or riser) given the other dimension (tread height or rise or tread depth or run).

The magic of using the Tangent function is that we can use that ratio to convert stair slope or angle in degrees to a number that lets us calculate the rise and depth or run of individual stair treads

• In roof speak 
  
  we describe this slope or ratio as roof slope (Rise / Run).
• In stair speak 
  
  we describe this ratio as (stair riser height / stair tread depth) or as (stairway total rise / stairway total run).
• In sidewalk and road building speak 
  
  we describe this ratio as the grade or percentage of slope (which is TAN x 100).

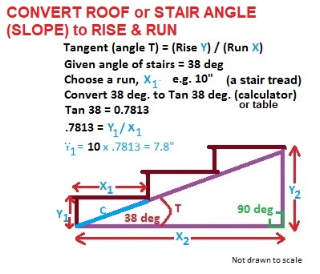
Here are two examples of roof pitch expressed as horizontal run and riser vertical change in height (rise) for a roof with a 38 degree slope: :

• On a 38 degree sloping roof (angle T) each individual vertical rise of 9.4" (Y₁) would have a horizontal run (X₁) of 12 inches.
• With a 38 degree sloping roof (angle T) with a rise of 7.8 feet to the center of the attic, (Y₂) would have total a run (X₂) of 10 feet. (In these calculations, as long as we keep the same unit for both rise and run we can change among inches, feet, meters, or roofing hammer handle lengths - whatever.

The magic is that the tangent ratio of the rise over run (Y/X) for roofs with different run lengths would always be the same - because they are built to the same slope or angle. You can see that reflected in our drawings above.

For a special use of right triangles to square up building framing,

also see FRAMING SQUARE UP 6-8-10 RULE - a simple method for assuring that framing members have been set at right angles to one another.

Find & Use the Tangent For Slope / Pitch Calculations

Watch out: when using a scientific calculator to obtain a tangent value, enter the angle in degrees as a whole number such as 38, not 0.38 or some other fool thing.

The TAN function or table can be used to convert a road grade or roof slope or stair slope expressed in angular degrees to rise if we know the run, or run if we know the rise ONLY because we are working in the special case of a right triangle.

That is to say, one of the angles of the triangle must be 90deg.

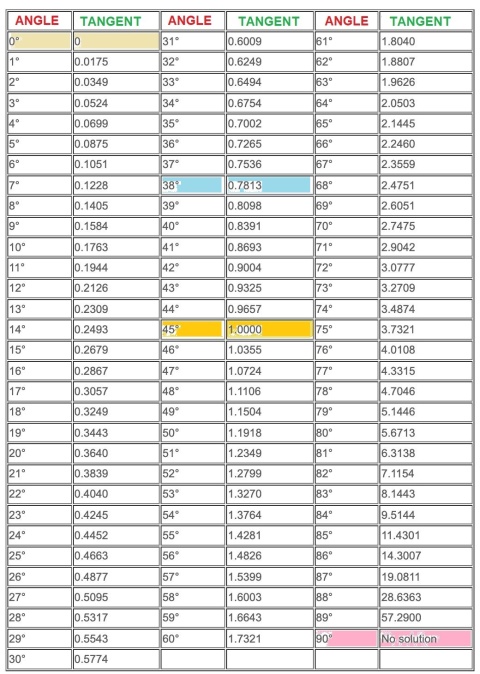
You can also find free tables of every trigonometric function online, such as a tangent table that will give the value of the tangent for any angle.

[Click to enlarge any image]

Table of Tangent Values for Each Angle in Degrees

Just type "tangent table" into your search engine and you'll find a table something like the one we show below.

To convert a slope (degrees) into rise/run (distance) is to use the tangent of that slope or angle

That number, a constant, lets us calculate rise if given run (say using a foot of run) or run if given the rise amount.

Tangent Value Table Converts Tangent to Angle

In the illustration at the start of this article, the tangent T of the 38 degree angle (the roof slope) is the ratio:

Roof Rise (Y₂) / Sloped Roof Run (X₂)

So we write the tangent of angle A as:

Tan <A = Rise (Y₁) / Run (X)

Our sketch above shows how we calculate the rise per horizontal foot (12 inches) of run when we are given the roof slope in degrees (or as the roof pitch or angle expressed in degrees).The purple sloped line is the sloping roof surface or the slope or angle of a stairway.

Standard rise & run:

Roof slope or stairway slope are properly expressed as inches of vertical rise per foot or 12 inches of horizontal run or distance traveled.

Other rise or run numbers:

Luckily, using the Tangent function, and given the angle of any stair or roof, we can calculate the amount of rise for any horizontal distance.

For example, how tall will a step riser be if our stairway is built on a 38 degree angle and if our horizontal distance or run is something other than 12" ?

In our sketch the vertical red line labeled (Y₁) shows the rise for the first stair tread. We chose a 10-inch horizontal "run" for the stair walking surface and we used the Tan function to figure out what the actual step rise will be.

It was trivial - I skipped digging into geometric calculations. I just took the given roof slope of 38 degrees and used my calculator (or a table, or actual geometry) to look up the value of Tan < A.

Tan 38^o= 0.7813

Now using the formula above

0.7813 = Rise (Y₁) / Run (X)

We just rearrange the equation following the basic rules of algebra to find Rise Y₁.

0.7813 x Run (X) = Rise (Y₁)

We could now calculate any total rise we want.

In the sketch we calculated the rise for 12" of run - and found that the answer was 7.8" - a step rise that's just OK.

Suppose instead we want to calculate the standard rise for 12" of run:

0.7813 x 12" = 9.4"  rise per foot of run

The calculations in this show the total rise in inches (Y₁) for every (X₁₎ or foot or 12" of horizontal run will be about 9.4" (actually 9.3756").

Heck we could calculate the total rise in the roof over say half the total width of the attic - that is the distance from the eaves to just under the ridge - that would tell us if I can stand up in the center of the attic of a roof with a 38 degree slope - for a given building width.

How to Check the Tangent of a 12 in 12 slope: Tan 45^o

As a sanity check we confirm that the tangent of 45 degrees is 1, or that two opposed 45 degree or 12 in 12 slope roof surfaces will form a 90 degree angle where they meet at the ridge, and will form 45 degree angles where they meet the wall top plate (or with respect to any horizontal line in the building).

Tan 45^o = 1.00 

Which is the same as saying a 45 degree slope = a 12 in 12 slope, or the roof will rise 12" for every 12" of horizontal run.

We used this detail to calibrate our folding carpenter's rule scale for reading roof slope from the ground.

Details of that procedure are

at ROOF MEASUREMENTS.

---

---

ADVERTISEMENT

---

---

Reader Q&A - also see RECOMMENDED ARTICLES & FAQs

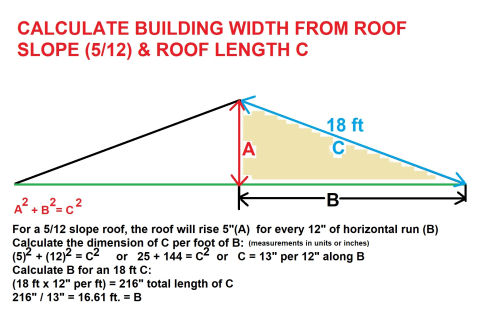
Illustration of a 5/12 roof showing calculation basics

On 2018-10-06 by bp - What is the RISE at 3 Degree pitch at 2200 mm & 4800 mm?

What is the RISE at 3 Degree pitch at 2200 mm & 4800 mm

On 2018-10-06 by (mod) - What is the RISE at 3 Degree pitch at 22ooMM & 4800Mm

Using any geometry book or online table of tangent values we will find the tangent of 3 degrees

What's a "tangent" - it's a fraction, expressed as a decimal value, that we can get for the ratio of two sides of right triangle: the tangent of angle X is

Opposite Side Length / Adjacent Side Length for the angle X

(At the companion article we cited at the start of this page we also show how to calculate tangents but we'll skip that for now)

For your 3 degree slope case:

tangent(3°) = 0.05241

Therefore for your roof,

0.05241 = Rise / Run

If I assume the two numbers you gave, 2200 mm and 4800 mm, are horizontal distance or "run", then we can solve the equation by simple algebra, writing

0.05241 = Rise / Run where run = 2200

0.05241 = Rise / 2200

2200 x 0.05241 = Rise

115.302 = Rise

and
0.05241 = Rise / Run where run = 4800

0.05241 = Rise / 4800

4800 x 0.05241 = Rise

251.568 = rise

On 2018-10-30 by sarmad - find the best curve junction

How to find the best curve junction if x=1.7 m and angle 15 degree ?

On 2018-10-31 by (mod) - How to find the best curve junction if x=1.7 m and angle 15 degree ?

Sarmad, from Wikipedia we have

Curvature is usually measured in radius of curvature.

A small circle can be easily laid out by just using radius of curvature,

But if the radius is large as a km or a mile, degree of curvature is more convenient for calculating and laying out the curve of large scale works like roads and railroads.

By this method curve setting can be easily done with the help of a transit or theodolite and a chain, tape or rope of a prescribed length.

In an n-degree curve, the forward bearing changes by n degrees over the standard length of arc or chord.

The usual distance in North American road work is 100 feet (30.48 m) of arc.[2] North American railroad work traditionally used 100 feet of cord and this may be used in other places for road work. Other lengths may be used—such as 30 metres or 100 metres where SI is favoured,

or a shorter length for sharper curves.

Where degree of curvature is based on 100 units of arc length, the conversion between degree of curvature and radius is

Dr = 18000/π ≈ 5729.57795,

where D is degree and r is radius.

On 2018-10-31 by (mod) - can we convert roof angle or slope to degrees of curve?

We don't normally convert roof slope or angle in degrees to degrees of curvature, since roofs are usually built in a straight line, not a curve, but it's possible to do so.

In the article above we discuss converting a slope or angle to degrees of angle where I state

The TAN function can be used to convert a road grade or roof slope expressed in angular degrees to rise if we know the run, or run if we know the rise ONLY because we are working in the special case of a right triangle - that is, one of the angles of the triangle must be 90deg.


And from Wikipedia we have

Curvature is usually measured in radius of curvature.

A small circle can be easily laid out by just using radius of curvature,

But if the radius is large as a km or a mile, degree of curvature is more convenient for calculating and laying out the curve of large scale works like roads and railroads.

By this method curve setting can be easily done with the help of a transit or theodolite and a chain, tape or rope of a prescribed length.

In an n-degree curve, the forward bearing changes by n degrees over the standard length of arc or chord.

The usual distance in North American road work is 100 feet (30.48 m) of arc.[2] North American railroad work traditionally used 100 feet of chord and this may be used in other places for road work. Other lengths may be used—such as 30 metres or 100 metres where SI is favoured,

or a shorter length for sharper curves.

Where degree of curvature is based on 100 units of arc length, the conversion between degree of curvature and radius is

Dr = 18000/π ≈ 5729.57795,

Source: Wikipedia 2017/10/31, original source: en.wikipedia.org/wiki/Degree_of_curvature

 

...

Continue reading at ROOF SLOPE DEFINITIONS or select a topic from the closely-related articles below, or see the complete ARTICLE INDEX.

Or see ROOF SLOPE CALCULATION FAQs - questions and answers posted originally on this page.

Or see these

Recommended Articles

• CALCULATE RISE & RUN from SLOPE in DEGREES - for ramps, roofs, stairs, walks, etc.
• FOLDING RULER ROOF SLOPE CALIBRATION
• FRAMING TRIANGLES & CALCULATIONS
• FROGS HEAD SLOPE MEASUREMENT
• HOPPUS MEASURER
• LOW SLOPE ROOFING
• PRINTABLE PROTRACTOR [Image file]
• RAMP SLOPE or PITCH
• ROOF AREA CALCULATIONS
• ROOF MEASUREMENTS - all methods for measuring roof slope, area, etc.
• ROOF SLOPE CALCULATIONS
• CALCULATE RAFTER LENGTH from SLOPE & RISE
• CALCULATE ROOF HEIGHT from SLOPE & RUN or BUILDING WIDTH
• CALCULATE ROOF TRUSS LENGTH FROM ROOF RISE
• CONVERT PERCENT GRADE to ANGLE or SLOPE
• CONVERT ROOF SLOPE or ANGLE in DEGREES to RISE or RUN
• ROOF SLOPE DEFINITIONS
• ROOF SLOPE TABLE, TYPES, WALKABILITY
• SHRINKAGE & HEIGHT CHANGES, LOG WALL
• STAIR ANGLE & SLOPE
• TANGENT & SLOPE CALCULATIONS

Suggested citation for this web page

TANGENT & SLOPE CALCULATIONS at InspectApedia.com - online encyclopedia of building & environmental inspection, testing, diagnosis, repair, & problem prevention advice.

Or see this

INDEX to RELATED ARTICLES: ARTICLE INDEX to BUILDING ROOFING

Or use the SEARCH BOX found below to Ask a Question or Search InspectApedia

Ask a Question or Search InspectApedia

Try the search box just below, or if you prefer, post a question or comment in the Comments box below and we will respond promptly.

Note: appearance of your Comment below may be delayed: if your comment contains an image, photograph, web link, or text that looks to the software as if it might be a web link, your posting will appear after it has been approved by a moderator. Apologies for the delay.

Only one image can be added per comment but you can post as many comments, and therefore images, as you like.
You will not receive a notification when a response to your question has been posted.
Please bookmark this page to make it easy for you to check back for our response.
Our Comment Box is provided by Countable Web Productions countable.ca

Citations & References

In addition to any citations in the article above, a full list is available on request.

---

ADVERTISEMENT

---