 Use Triangles & Simple Geometry to Aid Building Framing
Use Triangles & Simple Geometry to Aid Building Framing
How to square up decks, floors, roofs, walls or set stair rise & run
- POST a QUESTION or COMMENT about using triangles & simple plane geometry to square up buildings or to construct stairs
Triangles & geometry in building framing:
This article describes how we can use a simple tape measure and basic aritematic in framing a building deck, floor, wall or roof to get it square and straight. We explain how to use simple measurements & the 6-8-10 rule to square up building framing, decks, roofs, stairs, walls, even windows & doorways.
We also explain how to build a stair or other structure over sloped or "un-level" ground, how to calculate stair tread depth or riser height from stairway slope in degrees, and we discuss stair step rise & run calculations when we are given only the slope of a stairway.
Finally, we explain how to use TAN, the tangent function to convert a measured angle into stair step rise & run dimensions.
InspectAPedia tolerates no conflicts of interest. We have no relationship with advertisers, products, or services discussed at this website.
- Daniel Friedman, Publisher/Editor/Author - See WHO ARE WE?
3-4-5 or 6-8-10 Rule Squares Up Stairs, Roofs, Walls, Decks
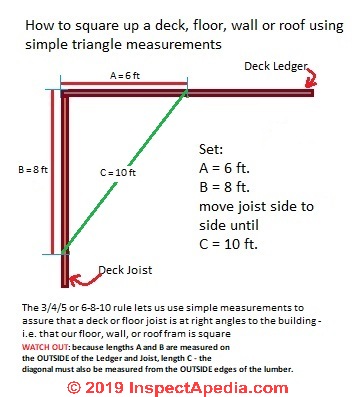 We use this basic right triangle function a2 =b2 +c2 in deck building to be sure that we are placing the deck sides at right angles to the building by using what my carpentry teacher (Bernie Campbalik) called the 6-8-10 rule.
We use this basic right triangle function a2 =b2 +c2 in deck building to be sure that we are placing the deck sides at right angles to the building by using what my carpentry teacher (Bernie Campbalik) called the 6-8-10 rule.
We will also discuss stair step rise & run calculations when we are given only the slope of a stairway, and we explain how to use the tangent function to convert a measured angle into stair step rise & run dimensions.
Article Contents
- 6-8-10 RULE QUICK SUMMARY - 3 measurements will get two framing members at a perfect right angle - 90°
- BUILD STAIRS OVER UNEVEN GROUND - how do we start or end stairs onto an uneven surface that slopes right or left?
- CALCULATE RISE & RUN from SLOPE - stair tread depth or riser height calculated from stairway slope in degree
- CALCULATE STAIR STRINGER LENGTH - to support our stairway
- TANGENT - what a Tangent and what's one good-for? - in stair construction
- USE Arc-Tangent or Arctan to CALCULATE ANGLE or SLOPE from RISE & RUN
3 Step 6-8-10 Procedure
OK so you're yelling "JUST TELL ME and SKIP the THEORY"
Let's go, using the sketch above and building a deck frame as an example we square up the structure in just 1 easy steps:
- Measurement A - 6 ft:
From one corner of where the deck will be bolted to the building (or from the end of the deck ledger already bolted in place, measure six feet in from one end of the ledger and mark that point. - Measurement B - 8 ft:
Then measure eight feet out from the building along your proposed deck side joist and mark that point on the inside of the joist. - Set Distance C to 10 ft:
Now measure the distance between point 1 and point 2 - a diagonal line between the deck side joist and the ledger board.
Move the side joist as necessary to make the diagonal line exactly 10 feet and you are guaranteed that the side joist is at a perfect right angle to the building - a nice way to decide how to locate deck corner post piers.
The 6 8 10 framing square-up rule works because (62 + 82) = 102 or 36 + 64 = 100. But that's enough plane geometry for now.
Complete details for squaring up a structure and making it level and plumb are found
...
Mathematical Approach to Building Stairs Spanning Uneven Ground
The geometry approach to calculating stair rise and run over rough terrain when you have only two measurements works correctly provided you know enough triangular geometry to convert between your sloped-line measurement (the hypotenuse of the triangle) and the triangle's other sides that form the rise & run dimensions.
Using a calculator and it's square root function, and the most basic knowledge of geometry is not enough - we also need a table of sine and cosine values, functions readily found these days online. [45]
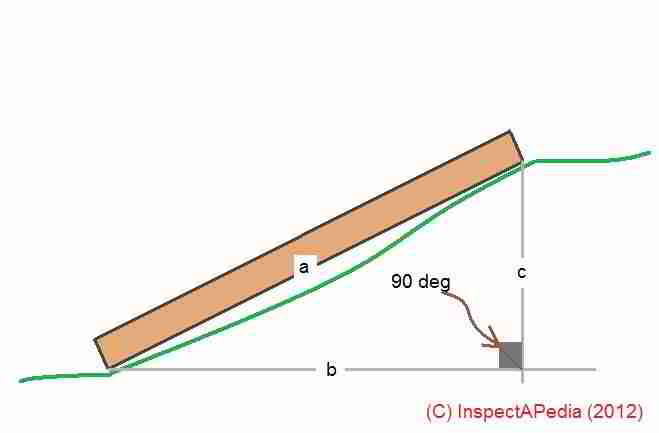
a2 =b2 +c2 - the square of the length of the hypotenuse (a) equals the squares of the lengths of the opposite sides of a right triangle (b) and (c).
In a geometry or trigonometry text you'll see that when we refer to the angle ab we mean the angle formed at the intersection of lines a and b, or in this case the lower left angle in our sketch.
And so the three angles formed by the triangle's sides are ab, bc, and ac.
Knowing that the triangle abc will always include a 90 degree right angle ( i.e. this is always a "right triangle"- angle bc in our sketch) allows use of sine and cosine tables to obtain the lengths of the two unknown sides b and c in the sketch.
Geometry teaches that if we know three pieces of data about a right triangle (one side length and two angles, or two side lengths and one angle) we can obtain all of the other data about a triangle - all of its angles, and the actual lengths of all of its sides.
sin of angle ab = (length of the opposite side c / the triangle's hypotenuse a) = a / c
cos of angle ab = (length of the adjacent side b / the triangle's hypotenuse a) = b / a
But the rub is that we need to know at least two of the angles on this triangle. We know bc is always 90 degrees. On the ground we'd have to measure either angle ab or angle ac.
You can do this using a transit, a protractor or other angle measuring tool either by placing your angular measuring tool on the sloped surface of the stringer side a, or by actually measuring the angle formed between side a and a horizontal or level surface.
Our carpenter's square at left is one such tool, though there are some neat level tools that, placed on a slope, will simply give you the angle directly as a readout.
Example: if our stairs are to run from the two extreme ends of the 2x stringer we illustrate at above right, and if that length (after cutting to "fit" the hill and desired stair run) measured 100 inches exactly, using just that known length of the hypotenuse of the triangle we would obtain the key measurements of stair rise c and stairway run b by first converting all measurements to inches and then using a table of sine and cosine values. Suppose we measure angle ab (sketch above) at 30 degrees.
sin of angle ab = (length of the opposite side c / the triangle's hypotenuse a) = a / c = 100 / c
cos of angle ab = (length of the adjacent side b / the triangle's hypotenuse a) = b / a = b / 100
Reading from sine and cosine tables, we'll find that side c (rise) = 50" and that side b (run) = 86.6"
If you don't think this whole sine-cosine process is absolutely horrible for field use in building a set of stairs then we're not on the same planet.
...
How to calculate stair tread rise & depth from stair slope measured in degrees
If I know the stairway slope how do I convert that to Rise per Foot of Run?
Stairway at 38 degrees: what is the rise and foot? - George Tubb
Reply:
George we're back to plane geometry. It's not really that bad if we just realize this is simple plane geometry that defines the relationships between a right triangle (that means one angle of the triangle is set at 90 degrees) and the lengths of its sides.
A generalized example of the explanation below is given
where we explain that you can easily convert any slope (roof, road, or stair) into rise or run distances using the Tangent function.
In geometry, if we know the lengths of sides of a triangle, we can calculate its angles. If we know two of its angles we can calculate the lengths of its sides. Etc.
The slope of your stairs is given as 38 degrees. And we figure that in calculating (or measuring) the "rise" of a stairway we can assume we are not so stupid as to not hold our tape vertical between floors - so we can assume the other known angle is 90 degrees - we've got a nice "right triangle".
You are asking the rise and "run" of the treads. There is no single answer, since we could choose different tread depths or "runs" that would give different tread rises or heights. E.g. we could make the stairs "one giant step" or "three little steps".
But to stay within reason, we can pick a desired step run or depth or step height or rise, and calculate the second number with the help of a calculator that will convert an angle in degrees using the Tan (tangent) function.
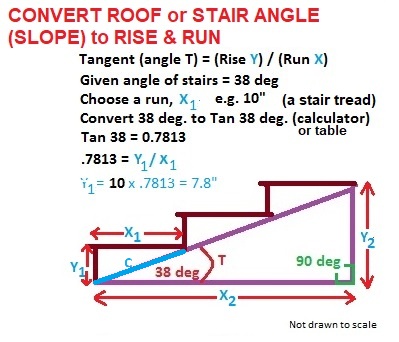
Choosing a stair tread depth (step run length) of 10" in the equation above gave us a calculated individual step rise of 7.8". That is, on a 38 degree sloped stairway, we will ascend 7.8" in height for every 10 inches of horizontal distance traveled.
If we chose instead to use a stair tread individual rise of 7.0" we would calculate as follows:
0.7813 = 7.0" / X1
X1 x (0.7813) = 7.0"
X1 = 7.0" / (0.7813)
X1 = 8.9" step run or tread depth.
This is not a good tread depth (too narrow) which reflects that basically, a 38 degree slope stairway is too step for comfortable climbing and forces us to have either treads that are too shallow or risers that are too high.
...
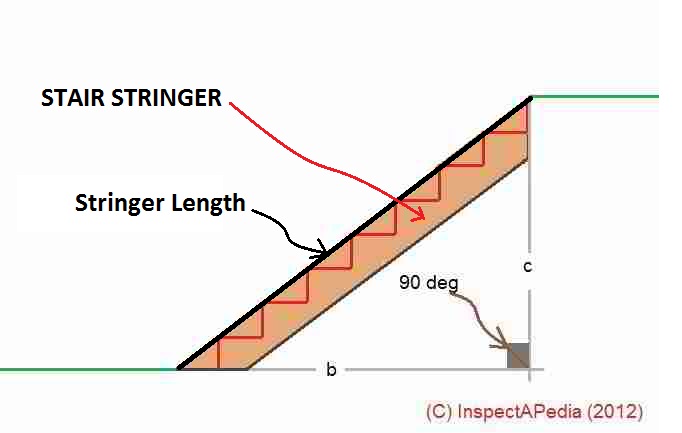
How to Calculate the Length of a Stair Stringer
Question: my riser is 116" how many stairs do i need and how long will my stringer be
(June 29, 2016) Anonymous said:
my riser is 116" how many stairs do i need and how long will my stair stringer be
Reply: first calculate the uniform step riser height for your stairs
Divide your total rise height (say 116") by a typical step riser (say 7") and get 16.5. As I used just 7" rise, I'll round down the number of risers from 16.5 to 16.
Ok so that's 16 steps up.
Now divide 116 / 16 = 7.25 - that's your uniform step riser height.
Next calculate the stair run length by multiplying the number of stair treads by total tread depth in inches
The formula for calculating the different sides of the stair triangle is given in the article above.
Let's use a 12" stair tread depth to start as it makes calculation more trivial.
16 steps (risers) x 12" tread = 16 feet of horizontal run.
Now we know two sides of the triangle:
16 ft. horizontal run or the bottom of the triangle. or 16 x 12 = 192".
16 steps up or vertical rise or 16 x 7.25" = 116".
Last calculate the stringer length as the hypotenuse of the stair triangle
For any right triangle, as we say in the article above
a2 =b2 +c2 - the square of the length of the hypotenuse (a) equals the squares of the lengths of the opposite sides of a right triangle (b) and (c).
If we let a = the sloping line or hypotenuse of the triangle, that's our stair stringer.
From there you can use your calculator to do the math to calculate your stringer length, right? If not let me know.
a2 + b2 = c2 for any right triangle.
So let
a = rise
b = run
c = the hypotenuse of the triangle or stringer length
Add a2 + b2 = c2 = your stringer length squared, then use your calculator to compute the square root of that number to get the actual stringer length.
Watch out: before cutting your stair stringer to length, be sure the stringer length or hypotenuse of your right triangle is the upper or "top" line (the heavy black line) in our sketch below:
Else you must remember to allow for the plumb-cut at the stringer top end where it will abut and be secured to a vertical framing member face such as a deck rim joist or a floor joinst, and allow for the plumb cut on the stringer bottom end where it must rest parallel to the floor or landing surface.
...
So What's a Tangent Anyhow?
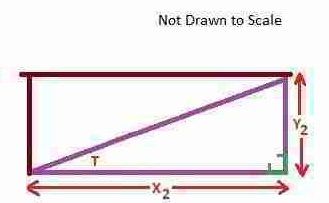
A tangent is the ratio of two sides of a right triangle: specifically the height (Y) divided by the base or length (X).
For any given stair slope (or angle) or triangle slope (angle T or "Theta" as we say in geometry class), that ratio remains unchanged.
Or in geometry speak:
Height Y1 / Length X1 = Height Y2 / Length X2
as long as we keep the slope or angle unchanged.
The tangent function is a ratio of horizontal run X and vertical rise Y. For any stairway of a given angle or slope (say 38 degrees in your case) the ratio of run (x) to rise (y) will remain the same.
That's why once you set your stair slope (too steeply) at 38 degrees, we can calculate the rise or run for any stair tread dimension (tread depth or run or tread height or riser) given the other dimension (tread height or rise or tread depth or run).
The magic of using the Tangent function is that we can use that ratio to convert stair slope or angle in degrees to a number that lets us calculate the rise and depth or run of individual stair treads
Here are two examples of stair tread run (depth) and riser height for a stair with a 38 degree slope: :
- A 38 degree sloping stair (angle T) with each individual step of 7.8" rise (Y1) would have a run (X1) of 10 inches for each step.
- A 38 degree sloping stair (angle T) with one "giant" step of 23.4" rise (Y2) would have a run (X2) of 30 inches.
We represent this giant 23.4" (ridiculously) tall step in our sketch above. You can see that the triangle and angle are unchanged.
The magic is that the ratio of the rise over run (Y/X) for both sets of stairs would always be the same - because they are built to the same slope or angle. You can see that reflected in our drawing above.
For a special use of right triangles to square up building framing, also
see USE the 6-8-10 RULE - a simple method for assuring that framing members have been set at right angles to one another.
Could we calculate the tangent of 38 degrees?
Well it's easier to use a scientific calculator or a TANGENTS TABLE and just ask for the Tangent of a known angle
If we knew that we had a triangle of 38 degrees at angle T (Theta) and if we knew two specific measurements X and Y we could indeed calculate T = Y/X.
After all, the tangent of angle Theta is the ratio of Y/X.
I used an online calculator available at http://www.creativearts.com/scientificcalculator/ and the simple formula shown in my illustration.
We chose (to make the math easy) a run of 10 inches - that's your tread depth shown as the blue X at the left end of the sketch.
The tread rise (for which we are solving the equation) is the blue Y at the left of the sketch. Just to make clear that we're simply working with a "right triangle" I show X and Y again as the horizontal and vertical sides of the triangle respectively.
I got also some help (a refresher on geometry) from Ferris High school's excellent geometry department who provides a more detailed analysis of the same problem as that posed by George Tubb's question.[17]
For a table of tangent values for all whole number angles
see TANGENTS TABLE
...
How to use Arc-Tangent or Arctan to compute slope or angle from rise and run of a stair or other slope
Those Ferris High kids in Spokane can also show you how to work this problem in the other direction: that is, if we know the rise and run of the stair we can calculate its slope or angle in degrees by using the arctangent function, as can a plethora of geometry websites.
We also took a look at MathisFun(advanced) cited atReferences or Citations to review the SOHCAHTOA trick for deciding which triangle side lengths and which trigonometry function to use to find the angle of a set of stairs when we know, as we usually do, the rise and run lengths of the stairway.
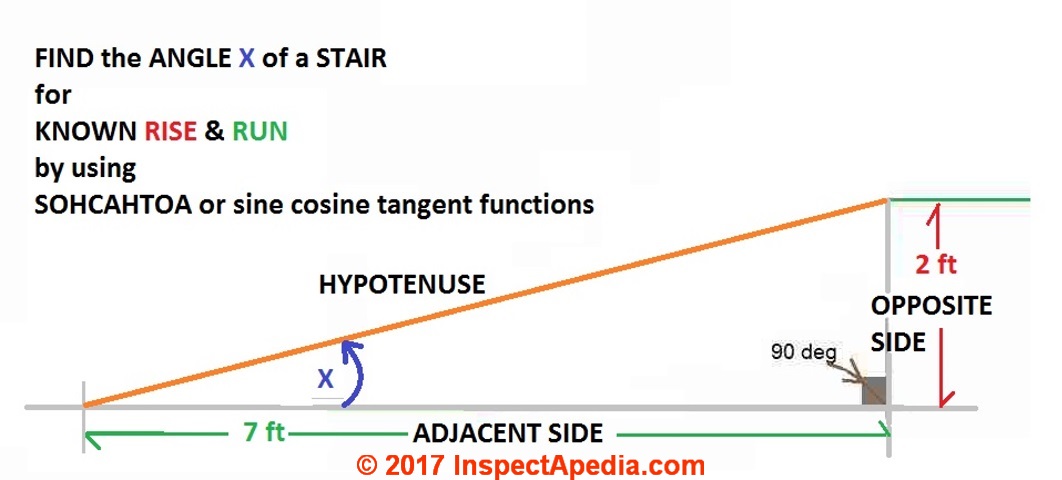
Question: what is the angle of my stairs if there is a 2 ft. rise and a 7 ft. run?
If I have a 7ft run, with 2 ft rise , what is the angle? - Ralph
Reply:
If we know the rise and run of the stair we can calculate its slope or angle in degrees by using the arctangent function.
Or in general to find an angle in a right triangle we start using the easier sine, cosine, or tangent functions.
Your stair rise is 2ft.
Your run is 7ft.
What if we want to find the angle of the stairs from JUST the RISE and RUN lengths?
We'll call the rise of 2 ft rise of the stair triangle OPPOSITE side (because it's opposite the angle we want to find)
We'll call the run of 7 ft. run of the stair triangle ADJACENT side (because one end of it touches the angle we want to find. (The other end touches the 90 degree right angle where it abuts the opposite side - the vertical line or rise.
The long side - the actual passage of the stairs upwards or downwards is the hypotenuse of the right triangle
A trick described by lots of geometry teachers is SOHCAHTOA a phrase used to help figure out which geometry function to use to find the angle.
Where O = Opposite and H = HypotenuseHere are the three formulas, any of which could calculate the angle of a stairway or roof:
SOH = SINE = OPPOSITE / (divided by) HYPOTENUSE - to use this formula we could start with SOH = SINE (of the angle we seek) = 2ft / 7.2 ft = 0.278
CAH = COSINE = ADJACENT / HYPOTENUSE - to use this formulat we need to know the length of the hypotenuse of the right triangle formed by your stairs
For your numbers, since we know the HYPOTENUSE length is 7.28 we could use the SOH formula above
SOH = SINE (of the angle we seek) = OPPOSITE / (divided by) HYPOTENUSE
Using standard geometry for the 3 sides of a right triangle, a2 = b2+c2 we could calculate the length of the hypotenuse of your triangle as
the square root of 49+4 (we squared your two sides) or the square root of 53 = using a calculator square root function for quick answer, that's 7.28 - the length of the hypotenuse and we could in turn use the cosine function to translate those lengths into an angle.
TOA = TANGENT = OPPOSITE / ADJACENT - this is the nicest formula to use if we know the rise and run of the stairs:
Let's use TOA to avoid having to calculate the hypotenuse at all and to find the angle of your stairs:
TOA = Tangent (of the angle we seek) = OPPOSITE / ADJACENT side lengths
or if we call the angle we seek "x", then we can write
Tan(x) = 2 / 7 = Tan(x) = 0.286
To convert that calculated tangent into degrees we use Tan-1 or arctangent feature of geometry:
NOW whip out your calculator and take the arctangent, that is Tan-1 (that's how we write ARCTANGENT or atan) of the Tan(x) we calculated - that is how we will convert a tangent into degrees:
Tan-1 (x) = Tan-1 (0.287) = 15.96 degrees or 15.96°
Which is to say the angle of your stairs will be about 16 degrees.
Over at ROOF SLOPE CALCULATIONS where we include Definition & Uses of Tangent & Tan-1 when Working With a Right Triangle (building roofs, stairs, walks, or whatever) we also show how to calculate the tangent value rather than looking it up.
...
Reader Comments, Questions & Answers About The Article Above
Below you will find questions and answers previously posted on this page at its page bottom reader comment box.
Reader Q&A - also see RECOMMENDED ARTICLES & FAQs
How do I build 6-inch steps on a 36% angle?
If the floor high is 10' and want to build step at 36% angle, how much floor mesurement I need to consider? Or re-stating my question:
There is a 120'' high floor/ceiling and want to build a 6'' inch steps at 36% angle, what is the floor measurement I need? - On 2020-07-16 by Francisco Ramirez
Reply by (mod) - Here's the math to calculate the total run distance and then individual step tread depth for a 36% slope stair with 6" step rise and 120" total rise
Francusco
First we need to clarify your question: a 36% is not an angle. So I'll assume you meant a 36% slope.
Angles are measured in degrees such as 36°
Slopes can be expressed in either degrees or angles or in percent-slope.
Percent slope is easy to calculate: it's simply (Vertical Distance / Horizontal Distance) multiplied by 100
If an engineer or architect gives us a stair specification in slope we go to
STAIR CONSTRUCTION, LOW ANGLE % SLOPE - Find the Percent Slope & Angle of Low-Rise Stairway - to convert that to inches of rise per foot of run.
There you'll see all of the ways to do these calculations but let's just use your numbers and jump right in.
If you really meant that your stairs have to have a 36% slope
and you specified a 6-inch individual step rise, then we can do the simple math to calculate the horizontal run distance for your stair as follows:
Build 6-inch rise steps on a 36% slope with a total rise of 120"
120/6 = 20 so we know we need 20 steps to ascend 120 inches according to your question.
Now to spread those steps out to get a 36% slope
120" rise / RUN = 0.36
or
120" = 0.36 x RUN
or
120" / .36 = RUN
or
333" = total RUN - so your 36% slope stair will have a horizontal run distance of 333" or about 9.25 feet.
Finally, knowing the total horizontal run distance we can calculate the individual tread depth as
333" / 20 (steps up) = 16.65" tread depth
So hot dog! now we know your stair dimensions:
- Total rise 120"
- Total run 333"
- Step rise 6"
- Step tread depth 16.65" (which is pretty deep)
Also see CALCULATE RISE & RUN from SLOPE - stair tread depth or riser height calculated from stairway slope in degree
And also see STAIR RISE & RUN CALCULATIONS
How many steps up do I need for stairs with a 79" rise?
I have a total ride of 79 inches and a run of 120 in what would u recommend me to do
Sorry I meant I have a total rise off 79 inches an total run off 120 inches what would you recommend me to do - On 2020-06-06 by Javier Montenegro
Reply by (mod) -
Javier
To build stairs that climb a 79 inch total rise, starting with a typical 7-inch step rise for safe comfortable use, you'd need 11 steps.
With a minimum step tread depth of 11 inches (some inspectors might permit 10) you'd need 7 x 11 or 77 inches (or more) of horizontal run.
If you WANT a long horizontal run, you could drop the rise to a minimum of say slightly under 5 inches, you'd build (79 / 5 ) = 16 steps.
Why not just use an online calculator? What size board do I use for a stair stringer?
This is some very useful information. Why not just use a rise run calculator on-line to get the angels, slope, pitch?
I found some where you can simply plug in the rise and run and everything else is calculated for you.
What size boards do you recommend using for the stringer for outdoor stairs?
Thanks - On 2017-04-29 by Marty
Reply by (mod) - It's also useful to understand the basic simple math for stair calculations: at least as a sanity check
Of course one can use a calculator, Marty, though it's helpful to understand the underlying concepts. If I have a general idea or can do the rough math I might catch a gross calculator error made just because I inverted a fraction or pushed a wrong number button - measure twice, cut once, especially when you only have two stair stringer boards on hand.
For an outside stair stringer the stringer depth (2x?) depends on how you're building the stairs.If you use cleats and through-screw and cleat-fasten the stair treads then you have the full depth of the stringer and a short stair may get by with a 2x10;
but if you're notching the stringer you'll see that you can end up with just 2-3" of actual lumber carrying the stair treads.
In that case use a 2x12 and even then you might have to double it.
Please see details at STAIR STRINGER SPECIFICATIONS
What's the best way to build stairs with 5" riser and 18" tread depth for total rise of 12'3" ?
I am building exterior stairs with a riser height of 5"inches and run of 18"inches and going to a height of 12'3" inches in over all height gained.
Is there another, better method then build "box stairs" to do this with?
Thanks for any feed back, new to site but really enjoy reading here. - On 2016-11-01 by Robert Osborne
Reply by (mod): Better to go to 21 steps with a 7" rise per step
Robert:
I think by "run of 18" " you refer to the read depth from nose to riser. That makes sense to me when the rise is so small (just 5"). But going to a height of 12'3" = that's total stair rise height. I calculate:
12'3+ = 147" total rise
147 / 5 = 29.4 risers before rounding. If you go to 30 risers that gives an individual step rise of 4.9" which is really low. you could consider a more normal riser height in the 6-7" range.
If you used a 7" rise you'd have exactly 21 risers.
The total horizontal run of your stair is about 21 x 18" if you stay with those deep treads, giving a run of 378" (rather long) or if you went to say a 12" tread depth the total stair run will be 252".
But perhaps you're making shallow treads to make the stair more easily climbable for elderly or disabled stair users who don't like tall risers.
If I were designing these stairs, because of the relatively tall total rise (147" based on your starting measurement is 12.25 feet) I'd want to see an intermediate landing (as is required by some codes).
I'm not sure what you mean by "box stairs" so instead I just rambled off some interesting measurements. The usual definition of "box stairs" is a stairway that is enclosed on both sides by a wall, so that the stair stringers are not visible - they're in or enclosed in the sidewalls.
I don't see that that applies to outdoor stairways.
For example stairs to a deck or porch are often framed with open stringers using either a notched stringer or cleats as we describe in this article series. That's a much simpler design.
Of course you'll need a guardrail and handrail on both sides of an exterior stair unless one side runs along a building wall.
...
Continue reading at STAIR RISE & RUN CALCULATIONS or select a topic from the closely-related articles below, or see the complete ARTICLE INDEX.
Or see these
Recommended Articles
- 6-8-10 RULE to SQUARE UP ANY STRUCTURE
- ANGLE FINDER LEVEL
- CALCULATE STAIR TREAD DEPTH or RISER HEIGHT from STAIR SLOPE in DEGREES - use triangles & plane geometry to convert stair slope in degrees to tread depth & riser height
- CLAY TILE ROOF SLOPE
- ELECTRICAL CONDUIT BEND CONNECT TOOLS
- FOLDING RULER ROOF SLOPE CALIBRATION
- FRAMING SQUARE BRACE TABLE
- FRAMING SQUARE USER'S GUIDE
- FRAMING TRIANGLES & CALCULATIONS
- FROGS HEAD SLOPE MEASUREMENT use of both TAN and (TAN-1)
- HOPPUS MEASURER - from the days when nobody could do math
- LOW SLOPE ROOFING
- PRINTABLE PROTRACTOR [Image file]
- RAMP SLOPE or PITCH
- ROOF AREA CALCULATIONS
- ROOF MEASUREMENTS
- ROOF SLOPE DEFINITIONS
- ROOF SLOPE CALCULATIONS Definition & Uses of Tangent & Tan-1 - Working With a Right Triangle (to build roofs, stairs, walls, walks)
- SQUARE PLUMB & LEVEL A STRUCTURE
- STAIR ANGLE & SLOPE
- STAIR CONSTRUCTION IDEAL DIMENSIONS
- STAIR RISE & RUN CALCULATIONS
- TANGENT & SLOPE CALCULATIONS
Suggested citation for this web page
FRAMING TRIANGLES & CALCULATIONS at InspectApedia.com - online encyclopedia of building & environmental inspection, testing, diagnosis, repair, & problem prevention advice.
Or see this
INDEX to RELATED ARTICLES: ARTICLE INDEX to STAIRS RAILINGS LANDINGS RAMPS
Or use the SEARCH BOX found below to Ask a Question or Search InspectApedia
Ask a Question or Search InspectApedia
Try the search box just below, or if you prefer, post a question or comment in the Comments box below and we will respond promptly.
Search the InspectApedia website
Note: appearance of your Comment below may be delayed: if your comment contains an image, photograph, web link, or text that looks to the software as if it might be a web link, your posting will appear after it has been approved by a moderator. Apologies for the delay.
Only one image can be added per comment but you can post as many comments, and therefore images, as you like.
You will not receive a notification when a response to your question has been posted.
Please bookmark this page to make it easy for you to check back for our response.
IF above you see "Comment Form is loading comments..." then COMMENT BOX - countable.ca / bawkbox.com IS NOT WORKING.
In any case you are welcome to send an email directly to us at InspectApedia.com at editor@inspectApedia.com
We'll reply to you directly. Please help us help you by noting, in your email, the URL of the InspectApedia page where you wanted to comment.
Citations & References
In addition to any citations in the article above, a full list is available on request.
- "Finding an Angle in a Right Angled Triangle", retrieved 2017/04/07, original source: https://www.mathsisfun.com/algebra/trig-finding-angle-right-triangle.html
- [27] "The Dimensions of Stairs", J. M. Fitch et al., Scientific American, October 1974.
- [28] Stair & Walkway Standards for Slipperiness or Coefficient of Friction (COF) or Static Coefficient of Friction (SCOF)
- ANSI A1264.2
- ANSI B101
- ASTM D-21, and ASTM D2047
- UL-410 (similar to ASTM D-21)
- NSFI 101-B (National Floor Safety Institute)
- NSFI Walkway Auditing Guideline (WAG) Ref. 101-A& 101-B (may appear as ANSI B101.0) sets rules for measuring walkway slip resist
- OSHA - (Dept of Labor CFR 1910.22 does not specify COF and pertains to workplaces) but recognizes the need for a "qualified person" to evaluate walkway slipperiness
- ADA (relies on the ANSI and ASTM standards)
- [45] "Right Triangle Angle And Side Calculator", csgnetwork, retrieved 9/29/12, original source: http://www.csgnetwork.com/righttricalc.html - Online sine / cosine functions permit calculation of lengths of sides of a triangle.
- In addition to citations & references found in this article, see the research citations given at the end of the related articles found at our suggested
CONTINUE READING or RECOMMENDED ARTICLES.
- Carson, Dunlop & Associates Ltd., 120 Carlton Street Suite 407, Toronto ON M5A 4K2. Tel: (416) 964-9415 1-800-268-7070 Email: info@carsondunlop.com. Alan Carson is a past president of ASHI, the American Society of Home Inspectors.
Thanks to Alan Carson and Bob Dunlop, for permission for InspectAPedia to use text excerpts from The HOME REFERENCE BOOK - the Encyclopedia of Homes and to use illustrations from The ILLUSTRATED HOME .
Carson Dunlop Associates provides extensive home inspection education and report writing material. In gratitude we provide links to tsome Carson Dunlop Associates products and services.