 Roof Area Calculations
Roof Area Calculations
Methods for calculating the area of a roof depending on what measurements you already know
- POST a QUESTION or COMMENT about types of roofing materials, installation, inspection, diagnosis, repair, maintenance, & warranties
Roof area calculation & measurement methods:
Here we describe various methods for measuring all roof data: roof slope or pitch, rise, run, area, and other features. We include on-roof measurements, roof measurements or estimates that can be made from ground level, and several neat tricks using a folding ruler to measure roof angle or slope.
This article shows how simple measurements can give the roof area without having to walk on the roof surface. This article series gives clear examples just about every possible way to figure out any or all roof dimensions and measurements expressing the roof area, width, length, slope, rise, run, and unit rise in inches per foot.
InspectAPedia tolerates no conflicts of interest. We have no relationship with advertisers, products, or services discussed at this website.
- Daniel Friedman, Publisher/Editor/Author - See WHO ARE WE?
How to Calculate the Area of a Roof
The attractive New Zealand slate roof shown here protects the beloved Catholic Church of St Werenfried in Waihi Village, at the edge of southern Lake Tekapo, in New Zealand (South Island).
Making one or two simple straightline measurements from the ground along with clever use of a folding rule or other methods discussed in this article series can give us accurate measurements of the church roof dimensions, slope, and area.
[Click to enlarge any image]
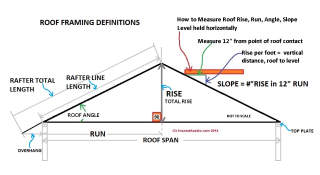
Definition of Roof Dimensions
Roof rise (b): first we will obtain the total roof rise by counting siding courses. We measure siding width & then we count courses at the building gable end. If we start counting siding at a horizontal lilne even with the lower roof edge or eaves and count up to the ridge, we've got a close guess at the total roof rise.
The number of siding courses from the roof triangle base to the roof peak x siding course width = total roof rise = (b)
Roof length (c): Measure or step off building gable end width.
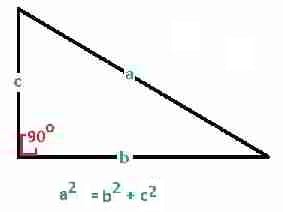
Roof width (a): This data allows us to calculate the roof triangle as we know two sides (b) and (c) of the three sides of a right triangle (the red lines in our photo at above left). Let (b) = the vertical rise in the roof and (c) = the roof length (building length + gable overhangs). The third side of the triangle, its hypotenuse or the sloping surface of the roof, or side is (a) which is calculated as follows:
a2 = b2 + c2 - the square of the length of the hypotenuse (a) equals the squares of the lengths of the opposite sides of a right triangle (b) and (c).
Given a2 we use our calculator to take the square root and bingo, we have the length of the sloping side of the roof.
Given that we now know all of the lengths of our triangle we can easily obtain roof slope too if we need it.
Now finally to get the roof area, we just need one more figure, the length of the roof along the building eaves or ridge. From the ground we measure or step off building length (L).
The roof area (RA) is calculated easily:
We multiply the Roof Length (c) (which is the sum of building length plus the gable end overhangs of the roof) by the Roof Width of slope (a) that we just figured out above when we computed the hypotenuse of the roof triangle (that's why we needed the roof rise number).
RA = (a) x (c)
We can use the TAN or tangent feature of a calculator or this TANGENTS TABLE as a trivial way to convert degrees of slope (or grade if we're building a sidewalk or road) into units of run per unit of rise.
The Tangent of any angle expressed in degrees is nothing more than a ratio:
Tangent = Rise / Run
How to calculate rise per foot of run for this roof using the number from an angle level
I'll show that even if we screw up we can still come out ok finding the angle and then the rise and run of a roof using the angle finding level.
I read 81 deg. on my angle level. Now let's figure run for 12" of rise for an 81 degree slope - HOLD ON! something's crazy here. This is a low slope roof, how can it be sloping 81 degrees? Egad! that's nearly straight up! This is a good lesson in thinking for yourself - or performing a sanity check on calculations.
The answer is I was holding my angle level on the wrong scale. I could have made my photos over again holding the angle level the right way, but there's an easier trick:
81 degrees is just 9 degrees off of dead vertical (90 - 81 = 9). So really I could go just 9 degrees off of flat. As "flat" is 0 degrees of slope, flat+ 9 = 9. My roof actually slopes 9 degrees. Whew!
The Tan value for my 9 degree slope roof = Tan ( 9) = 0.1583
Find Tan 9 deg using a handy dandy calclator, or a TANGENTS TABLE or as I illustrate also at
at ROOF MEASURE by FOLDING RULE.
The inches of rise for 12-inches of run on a 9 deg low-slope roof is calculated as follows:
Tangent is defined as a ratio: Rise / Run so all we need is a little algebra (don't faint, it's easy):
0.1583 = Rise / Run
Set run to 12-inches because we're going to calculate the rise per foot of run.
0.1583 = 12 / Run
Use simple algebra:
0.1583 x Run = 12" of rise
Run = 12" / 0.1583
Run = 75.8"
That makes sense: we travel about 75 inches horizontally for every 12 inches of vertical rise on this low slope 9 degree roof.
Calculate Unit Rise for the Roof Rise
To calculate total rise if I knew the total run (say we had made an on-roof measurement) we take the following steps:
Total Rise = (Total Run in Feet) x (Rise per Foot)
The Tan value for my 9 degree slope roof = Tan ( 9) = 0.1583
0.1583 = Rise / Run
Using a little high school algebra we can re-write the equation as
0.1583 x Run = Rise
If I want to know the rise per foot of run I calculate
0.1583 x 12 = 1.89 " of rise per foot of run.
Calculate Total Rise for the Roof
I measured the total horizontal run - my building width is 20 ft. + a total of 2 ft. of overhang at the eaves.
0.1583 x 22 = 3.5 ft.
My roof increases in height 3.5 ft. from the eaves to the high end (this is a shed roof).
I can check this result against the rise per foot we got above.
(22 ft. x 1.89" rise per foot) / 12 = 3.5 ft. (thank goodness)
For the Tangential Enthusiast - Usnig Inverse Tangent Function Tan-1
The inverse Tan-1 function can convert a Tan value back into degrees of roof slope.
Tan-1 (1.43) = 55 deg. and wonderfully, Tan-1 (1.00) = 45 deg.
Since Tan is a simple ratio of unit Rise / unit Run, we note that we can quickly convert a roof slope in degrees into the number of inches of rise per 12" of run as follows, using a 55 deg. slope as example:
Tan (55) = 1.43
Since 1.43 = rise / run we can use simple algebra to write:
1.43 x 12" run = 17.16" of rise per 12" of run
Summary of How Roof Measurements are Calculated
How to Measure or Estimate the Total Roof Area
If you have safe access to the roof surface you can quickly make the needed area measurements: just measure from the ridge to the lower edge or eaves, keeping your tape straight.
With a decent 3/4" or 1" wide 30 ft. tape measure you can extend the tape out to catch the roof eaves without having to walk dangerously close to the roof edge. Also measure the roof edge or length.
- RW = Roof Width = dimension from ridge to eaves. In my sketch I use (a) or the dimension of the sloping surface as RW. Remember to include in (a) the amount by which the roof extends out over the building walls - its eaves.
- RL = Roof Length = dimension of the roof from one gable end of the building to the other. You don't see RL in my sketch at left. RL is simply the building width plus the amount of overhang at the two gable ends of the building.
- RA = Roof Area = RW x RL
- Well this is only true provided the roof surface is a rectangle. If you are working with hips and gables and you want to get precise area measurements you may find it easiest to divide the individual roof slopes up into sub-components: a rectangular part and a triangular part.
- For a rectangle just multiply the width and length of its two sides to obtain area.
- For a right triangle, its Area = 1/2 x ( c x b )
- For a triangle such as the red example in our photo, just divide the triangle into two halves (green line) and you can still make these calculations with ease.
- Remember to keep your dimensions all the same (inches or feet).
Roofers measure or estimate the total roof area in square feet that is then converted to roofing squares - the unit of ordering of roofing material. One roofing "square" covers 100 sq.ft. of roof area. Convert roof area in square feet to squares of roofing material by dividing by 100.
- Roofing Squares = RA / 100
Watch out: do not walk on roofs that are fragile (you will damage the surface, make leaks, and make people mad.) Do not try to access a roof that is unsafe for any reason: height, slope, condition, wet, slippery, windy, etc. In those conditions you'll be better off making a few simple measurements from the ground level to figure the roof areas involved.
Estimating the Roof Area for Complex Roofs
Watch out: also that roof measurement is only trivial for simple shed or gable roofs whose slopes are a simple rectangle. For hipped roofs, mansards, and intersecting gables some simple triangles need to be measured if you want an accurate estimate of roof area.
Accurate Calculation of the Area of an Individual Roof Slope from Available Measurements
To be more accurate, and in cases where we need to get the roof area while working from the ground we can get the actual or accurate area of an individual roof slope as follows
- Measure the building length (BL) and width (BW)
- Get roof length: Measure or estimate the additional horizontal distance of roof overhang (eaves) at the building front (or rear) corresponding to the individual roof slope being calculated - Eaves Overhang Width (EOW)
- Measure or estimate the additional horizontal distance of roof overhang at the both left and right gable ends for the roof slope being calculated - Gable End Overhang x 2 = (GEO)
- Flat or Horizontal Projection of Roof Length = BL + GEO - this is also the true roof length = RLTrue
- Measure or estimate or calculate the roof rise - the height increase from the eaves to the ridge.
- Get roof width: Use the roof rise to calculate the true roof width as follows:
- From a right triangle a2 = b2 + c2 or hypotenuse
- RWTrue2 = Rise2 + RLTrue2
- Example: RWTrue2 = (6ft. rise)2 + (30 ft roof length)2
- RWTrue2 = 36 + 900
- RWTrue2 = 936
- SQRt of RWTrue2 = 30.6 ft.
- RWTrue= 30.6 ft.
- Calculate the Roof Area (RATrue) for the slope whose true dimensions were just calculated avove
- RATrue= RLTrue x RWTrue
- Example:
- RATrue= 30 x 30.6
- RATrue= 918 sq.ft. - I would roundup to 1000 sq.ft.
- Add 10% for wastage, add additional if needed for ridge or hip cap shingles. (You will need additional material depending on the type of roof covering material being used. Allow for errors, wastage, damaged shingles, for the shingle starter course and for hip and ridge cap shingles. )
- Calculate number of roofing squares of material: divide the roof area in square feet by 100 to obtain the needed number of roofing squares of roof covering material.
- Example: 1000 sq.ft. + .10 (1000) = 1100 sq.ft.
- 1100 sq.ft. / 100 = 11 squares for this roof slope.
- Add all of the roof slopes to obtain total roof area in square feet
How to Use Horizontal or "Flat" Roof Projections as Rough Estimates of Roof Area for Inaccessible Roofs
Another simplistic approach used by some estimators is to ignore complex roof structure, just measuring the building's footprint and the roof slope - an approach that gets you into the right "ballpark" but will very seriously under-estimage the roof area for steep slope roofs.
Frankly, as we illustrate beginning at ROOF MEASUREMENTS, there are some easy and accurate alternatives that can give a good estimate of roof area while making measurements only from the ground. But to understand how some people use a flat or horizontal projection of a roof to guess at roof area, here is the procedure.
BF: Measure the building footprint or BF
EO: Measure or estimate the increase in footprint size given by the roof eaves overhang. (Tip: look at the drip line under the roof eaves and measure the distance from the outer edge of the drip line to the building exterior wall. This is EF.
GO: Measure or estimage the increase in footprint size given by the gable end overhangs. This is GO.
RF: If the eaves overhang and gable end overhang are the same on both front and back and left and right building ends we just add these up to obtain Roof Footprint or RF.
RF = BF + (2 x EO) + (2 x GO)
RA: Obtain the approximate roof slope to convert Roof Footprint to Roof Area - RA using
the ROOF SLOPE MULTIPLIER TABLE given below.
RA = RF x Roof Slope Multiplier
All of the Ways to Get the Roof Slope
You can calculate the roof slope if you know just a few measurements. Details are
at ROOF SLOPE CALCULATIONS
You can estimate the roof slope from the ground by any of several methods described
at ROOF MEASUREMENTS
How to convert the building footprint or roof "footprint" (building footprint + roof overhangs) to roof area
To convert the rectangular footprint of the building roof to roof area we need to increase the footprint area to account for the greater area covered by the sloping roof. Using any of the roof slope estimating or measuring methods described above, just this simple roof slope multipication chart:
Roof Slope Multipliers: convert a "flat" or "projected horizontal" building footprint
|
|||||||
|---|---|---|---|---|---|---|---|
Roof Slope
or |
Multiplier to convert a flat horizontal
footprint to roof area |
Triangle side (a) Hypotenuse or Roof Length |
Triangle side (b) |
Triangle side (c) Hypotenuse or Roof Width SQRT (a2 = b2 + c2) |
Convert (c) to Inch Scale (convert fraction to 16ths of an inch) |
(c) x 2 (two roof slopes) |
|
| |
12 3/16" | 24 3/8" | |||||
| 12 3/8" | 24 3/4" | ||||||
| 12 5/8" | 25 1/4" | ||||||
| 13 " | 26" | ||||||
| 13 3/8" | 26 3/4" | ||||||
| 13 7/8" | 27 3/4" | ||||||
| 14 3/8" | 28 3/4" | ||||||
| 15" | 30" | ||||||
| 15 5/8" | 31 1/4" | ||||||
| 16 5/16" | 32 5/8" | ||||||
| 16 7/8" | 33 3/4" | ||||||
Notes to the table above
Notes: for fractional slopes, when estimating roof area use the next higher slope multiplier.
Roof Pitch = rise / run = Roof Slope = Tangent Function. Tangent calculations are illustrated
Roof slope or pitch can also be expressed in degrees or angular degrees, as we illustrate
The numbers in the table above can be calculated as follows: (and as illustrated below)
For a 12-inch unit-length roof we calculate the hypotenuse dimension to obtain the roof true width for each roof slope. In the table above the roof slope or rise (e.g. 6 in 12) gives us the vertical dimension of a right triangle. The horizontal dimension is fixed at 12 inches.
...
Continue reading at ROOF MEASUREMENTS or select a topic from the closely-related articles below, or see the complete ARTICLE INDEX.
Or see these
Recommended Articles
- CALCULATE RISE & RUN from SLOPE
- LOW SLOPE ROOFING
- ROOF AREA CALCULATIONS
- ROOF MEASUREMENTS
- ROOF SLOPE CALCULATIONS
- ARCTANGENT CALCULATES ROOF / STAIR ANGLE
- CONVERT PERCENT GRADE to ANGLE or SLOPE
- CONVERT ROOF SLOPE or ANGLE in DEGREES to RISE or RUN
- CALCULATE ROOF HEIGHT from SLOPE & RUN or BUILDING WIDTH
- CALCULATE RAFTER LENGTH from SLOPE & RISE
- CALCULATE the TAN VALUE from TWO SIDES of a TRIANGLE
- CALCULATE ROOF TRUSS LENGTH FROM ROOF RISE
- DEFINE & USE TANGENTS for BUILDING ROOFS, STAIRS
- ROOF SLOPE TABLE, TYPES, WALKABILITY
- ROOF SLOPE DEFINITIONS
- ROOF MEASUREMENTS - all methods for measuring roof slope, area, etc.
Suggested citation for this web page
ROOF AREA CALCULATIONS at InspectApedia.com - online encyclopedia of building & environmental inspection, testing, diagnosis, repair, & problem prevention advice.
Or see this
INDEX to RELATED ARTICLES: ARTICLE INDEX to BUILDING ROOFING
Or use the SEARCH BOX found below to Ask a Question or Search InspectApedia
Ask a Question or Search InspectApedia
Try the search box just below, or if you prefer, post a question or comment in the Comments box below and we will respond promptly.
Search the InspectApedia website
Note: appearance of your Comment below may be delayed: if your comment contains an image, photograph, web link, or text that looks to the software as if it might be a web link, your posting will appear after it has been approved by a moderator. Apologies for the delay.
Only one image can be added per comment but you can post as many comments, and therefore images, as you like.
You will not receive a notification when a response to your question has been posted.
Please bookmark this page to make it easy for you to check back for our response.
IF above you see "Comment Form is loading comments..." then COMMENT BOX - countable.ca / bawkbox.com IS NOT WORKING.
In any case you are welcome to send an email directly to us at InspectApedia.com at editor@inspectApedia.com
We'll reply to you directly. Please help us help you by noting, in your email, the URL of the InspectApedia page where you wanted to comment.
Citations & References
In addition to any citations in the article above, a full list is available on request.
- NRCA - National Roofing Contractors Association - Website: www.nrca.net 10255 W. Higgins Road, Suite 600, Rosemont, IL 60018-5607, Tel: (847) 299-9070 Fax: (847) 299-1183
- Asphalt Roofing Residential Manual from ARMA the Asphalt Roofing Manufacturers Association Website https://www.asphaltroofing.org/product/residential-asphalt-roofing-manual/ ,
- In addition to citations & references found in this article, see the research citations given at the end of the related articles found at our suggested
CONTINUE READING or RECOMMENDED ARTICLES.
- Carson, Dunlop & Associates Ltd., 120 Carlton Street Suite 407, Toronto ON M5A 4K2. Tel: (416) 964-9415 1-800-268-7070 Email: info@carsondunlop.com. Alan Carson is a past president of ASHI, the American Society of Home Inspectors.
Thanks to Alan Carson and Bob Dunlop, for permission for InspectAPedia to use text excerpts from The HOME REFERENCE BOOK - the Encyclopedia of Homes and to use illustrations from The ILLUSTRATED HOME .
Carson Dunlop Associates provides extensive home inspection education and report writing material. In gratitude we provide links to tsome Carson Dunlop Associates products and services.