Calculations you need to build stairs:

Here using simple arithmetic we explain how to make stair design calculations: number of steps, step riser height, total stair height or rise, total stair length or run.

We explain how total elevation change between two levels or floors (rise) and stair length (run) are used to calculate the right measurements when building indoor or exterior stairs to fit the building or the terrain.

Details of methods for accurate stairway rise & run measurement are provided for tough cases such as building a stair over steep slopes and irregular surfaces.

Stair Building Calculations: simple arithmetic for safe stair designs to fit any situation

Here we describe how to translate the stair rise and run into a specific number of stair treads and risers that will be uniform and of proper (safe) dimension.

We also describe how to design and build low-slope or low angle stairways with special consideration for tread and landing dimensions to avoid halting-walk stairs and other trip hazards.

This article includes example stair building calculations and warns about some "in between" stair tread sizes that may be a trip/fall hazard.

We also explain now to include landings and platforms in stair design calculations.

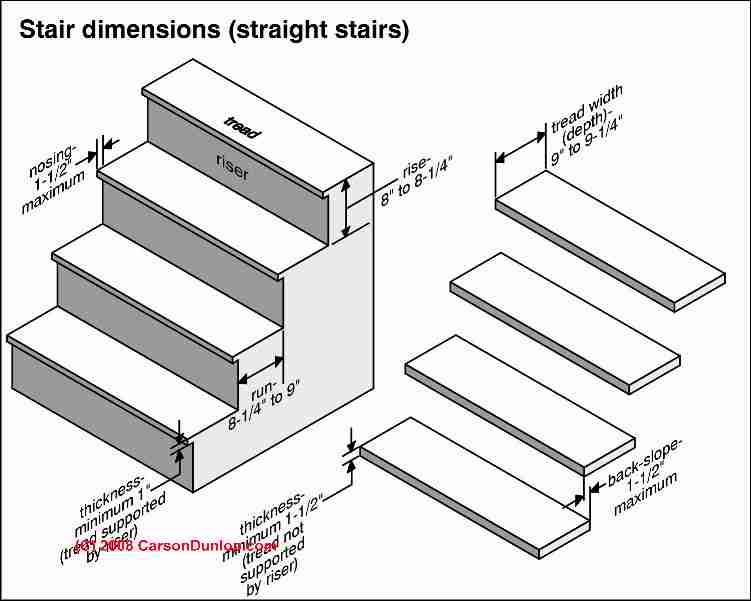
Finally, we also explain how to adjust factory-built or pre-fab stairs to the exact stair rise dimension in your installation. Page top stair dimension sketch courtesy of Carson Dunlop Associates, a Toronto home inspection, education & report writing tool company [ carsondunlop.com ].

Article Contents

• STAIR TREAD & RISER RULES of THUMB - basic numbers for stair building
• DEFINITION of STAIR RISE & STAIR RUN
• MEASURE STAIRWAY DIRECTLY DURING CONSTRUCTION - Direct Measurement of Rise & Run When Building Stairs
• STAIR CALCULATIONS by DIRECT LAYOUT on STRINGER - measure and mark stair tread locations on the supporting stringer
• STAIR RUN CALCULATION: NUMBER of STEPS
• STAIR RISE CALCULATION: NUMBER of RISERS
• STAIR PLATFORMS / LANDINGS
• ADJUST FACTORY-BUILT STAIR to FIT the SITE

Stair Tread & Riser Rules of Thumb

As a starting point in stair and step design and build you can calculate the step rise & run for a stairway with these rules of thumb.

Our photo illustrates construction of a low-slope stairway located in the "Jewish Quarter" in Girona, Spain.

These steps are several hundred years old, are worn, and have a bit of a slope to them.

• 1 Tread depth in inches + 1 Riser height in inches = 17" to 18"
• 7" riser & 11" tread depth is a starting target to use when calculating actual stair run and number of steps needed
• Stair slope or angle of about 37° which equals approximately a 75% slope
  
  The stair Angle or Slope should be between 30° and 50°, ideally around 37°
  
  I prefer a 33° stair that is approximately a 66% slope as is given by a 7/11 step rise/run ratio.
  
  See details at STAIR ANGLE & SLOPE
• FRAMING SQUARE UP 6-8-10 RULE given below helps square up stairs and stair openings
• STAIR DIMENSIONS, WIDTH, HEIGHT gives details of stair width, headroom, etc.
• STAIR CONSTRUCTION IDEAL DIMENSIONS gives additional stair building design starting point dimensions for stair or step rise, run, slope.
• RAILING CODES & SPECIFICATIONS gives the requirements for handrails and guardrails

Bernie Campbalik who taught us carpentry, including stair building, used a rule of thumb that basically makes the run longer when the rise is shorter.

I've seen several rules such as the sum of one tread and one riser should always be equal or greater than 17; or two treads plus one riser should add up to around 28 or 29.

The concept is that a low rise stair usually has, just as you suggest, a tread that provides a "longer" walking surface. Up to a point. If we make the rise too short (under 4 inches of rise) it's not a step at all, it's a trip hazard.

Generally we solve the problem of low slope long run stairways by using all platforms - steps that are 36" in length or more in the direction of run of the stairs, or by using a combination of normally sized stair treads (say 11" deep treads with a 6" or 7" rise) along with intermediate stair platforms.

And relevant to your question is the "depth" or run of each step in the direction of travel.

While generally it's good to use a deeper stair tread (treads less than 11-inches in depth are not recommended), there may be some intermediate depths (or step run) such as around two feet that make for awkward walking and may risk stair falls. A better stair design may involve increasing the rise and lengthening one or more steps into a platform of 36" or more of horizontal walking surface.

And of course long stair runs due to a very tall total rise (more than 12 feet) also is likely to require an intermediate stair platform as well.

See a complete set of stair construction rules of thumb at STAIR BUILDING RULES of THUMB

Watch out: make these stair "steps" long enough to avoid a halting-walk stair fall hazard.

See HALTING WALK STAIR DESIGNS for LOW SLOPES or SHORT STEP RISE

Definition of Stair Run & Rise

Definition of stairway run:

the run of a stairway is the total horizontal distance traveled by a walker using the stairs, from the face of first riser to the face last riser.

Definition of stairway rise (total stair height):

the rise of a stairway is the total vertical height of a stairway between the walking surface just before the first stairway tread or step up and the beginning of the horizontal walking surface reached at the top of the stairs. In the model codes such as the International Residential Code or IRC you'll see, where that code is adopted by various municipalities, total stair vertical rise guidelines such as the following:

R311.7.3 Vertical rise. A flight of stairs shall not have a vertical rise greater than 12 feet 7 inches (3835 mm) between floor levels or landings.

Between landings and platforms, the vertical rise is to be measured from one landing walking surface to another.

The limited height provides a reasonable interval for users with physical limitations to rest on a level surface and also serves to alleviate potential negative psychological effects of long and uninterrupted stairway flights.

This intermediate landing could also help someone stop if they fell on the stairway. - Source: STAIRS & HANDRAILS RESIDENTIAL CODE, CHAPTER 3, BUILDING PLANNING [PDF] Routt County Colorado Building Department, retrieved 2024/08/28, copy on file as Handrail-Stairway-Residential-Codes-IRC-Routt-County-CO.pdf

Don't confuse total stairway rise or height (given above) with individual stair step height or riser height that we discuss in detail

at STAIR RISER SPECIFICATIONS

Direct Measurement of Rise & Run When Building Stairs

Here is how you can measure the actual stair rise and run, followed by how to calculate the same data.

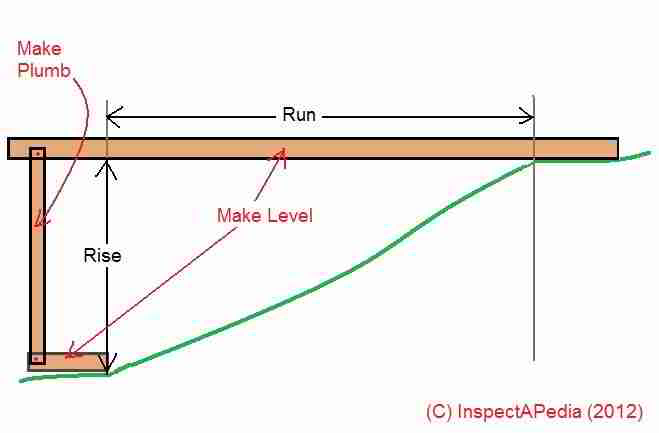
Our illustration above shows an example rise and run for a simple uniform-tread depth and riser height stairway. It's easy to measure the horizontal run and vertical rise for a stairway built between two parallel and flat surfaces - such as inside a building between two floors.

Simply extend a measuring tape down through the stairway opening in the upper floor and measure the distance between the surface of the upper floor or level and the surface of the lower floor or level. That will be the total rise.

But measuring the rise and run between two elevations that are not parallel and not flat, such as for an exterior stairway built over sloping ground can be more difficult (you cannot measure the vertical distance directly as we did above). If you're not careful you will make a measurement error, leading to miscalculations among total rise, run, and step and riser dimensions.

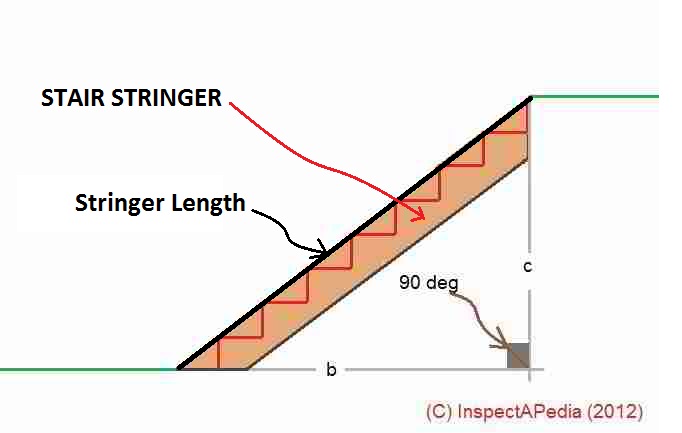
Stair Calculations by Direct Layout on the Stringer

What many stair builders do is simply lay a (hopefully straight) stair stringer between the two elevations, measure the actual rise and run distances, and lay-out the stair dimensions on the fly by measuring and marking along the side surface of the stringer.

The approach of placing a stringer along the desired stair slope, measuring and marking layout immediately on the stringer works acceptably if terrain shape permits and if you are careful with stair layout.

The direct stairway layout marking along the stair stringer is easy if we are building interior stairs between floors (sketch at left) or exterior stairs down a concave slope (sketch below left) but this approach won't handle a convex slope or concave (below right) unless we first excavate the hillside or raise the entire stair design and assembly to span above the high point on the slope.

For laying out stairs whose top and bottom landings are themselves not level surfaces

see STAIR DESIGNS for UNEVEN / SLOPED SURFACES.

For an easy way to measure the stair rise and run outdoors when the surface being climbed or descended (before your stairs are built) is uneven, see the sketch given just below

at STAIR RUN MEASUREMENT: NUMBER STEPS

How to Calculate the Stairway Run - Horizontal travel & Number of Steps

Definition of stair run or stairway run: the total horizontal distance that must be traveled in ascending the stairs between two levels.

Measure the total stair run. Indoors this is easy: Just make the measurement shown in our sketch above, measuring "Run" of the stairway as shown.

Watch out: don't just divide the horizontal run by your preferred tread depth (say 11") - instead you must calculate the number of steps in your stairway so as to assure that all of the steps have a uniform rise.

We'll do that next

at STAIR RISE MEASUREMENT: NUMBER of RISERS

The total stair run distance will allow you to mark or stake out the exact location of both the stair top first step and the stair bottom last step. Outdoors you will probably need top and bottom stair landings unless you're entering and leaving the stairs from an existing sidewalk or ramp.

For direct measurement of a total stairway run and rise outdoors over uneven ground, use straight lumber of sufficient length as shown in our next sketch below.

Watch out: be sure that your boards are at right angles to one another and that the vertical and horizontal boards are plumb and level. Otherwise your measurements will be wrong.

Complete stair tread dimensions and specifications are

at STAIR TREAD DIMENSIONS

How to Calculate the Stairway Rise & Number of Steps / Risers - Vertical Travel

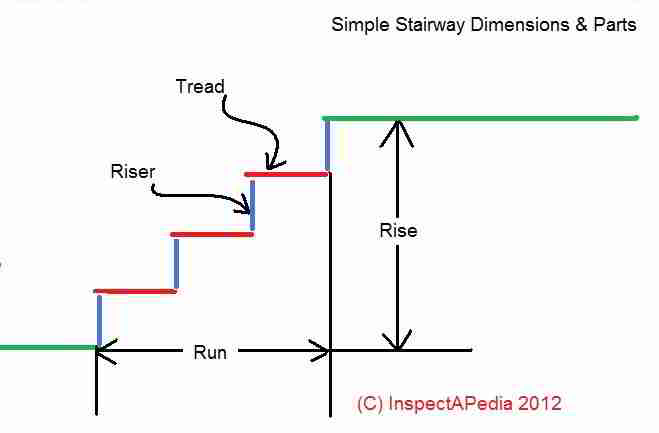Definition of stairway rise: the total vertical distance that must be traveled in ascending the stairs between two levels.

In our simple three tread four-riser stair sketch shown here you see the total rise is from lower walking surface to upper walking surface. Indoors that's floor to floor. Outdoors that's landing to landing.

Measure the total stair rise.

Indoors this is easy: Just make the measurements shown in our sketch above, measuring "Rise" - the vertical distance of the stairway as shown.

Above we suggested by sketch how you can measure the stair rise over uneven ground. Again it's critical that your measurement boards are plumb and level and square.

Calculate the number of step risers:

divide the total rise by a reasonable starting number for step riser height.

We use 7 inches as a reasonable stair riser height.

Watch out: don't forget to re-check check the riser height and actual number of steps against the horizontal run space to be sure your stair fits in the opening or space allotted.

And if your stair is indoors passing up through a cut-out opening in the floor above or outdoors passing through a multi-level deck or similar structure you will want to double check the headroom for your stairway too.

See STAIR HEADROOM.

What if the Total Rise is Not Evenly Divisible by my Step Height?

If your total rise is a multiple of 7 you're home free. That's unlikely. So now what?

Calculation example for real-world stair risers:

Total rise measured R = 75"

First calculation: Rise in inches divided by 7-inches

Divide the rise total by step riser height: 75/7 = 10.71 risers. But we can't have "part of a step" - don't try that or everyone will fall down the stairs.

We will either increase the number of steps by 1, shortening the stair rise, or decrease the number of steps by one, lifting the stair rise.

Then we spread the adjustment evenly over all of the stairs,

I would calculate both numbers - that's going to be 11 risers or just 10 risers - and choose the one that keeps my step rise closest to a comfortable height.

11-riser stair example

75" total height / 11 stair risers = 6.81" risers individual stair riser height - this is an acceptable step riser height.

10-riser stair example

75" total height / 10 stair risers = 7.5" risers individual stair riser height - this riser is acceptable in some jurisdictions and not others.

I would build these stairs using eleven steps each having a 6.8" riser. I could try to make my first or last step 0.01" taller as that variation is much less than the allowable 3/8", but frankly you'll never sense or feel that 1/100th of an inch accuracy. Forget it.

Handling Larger Stair Riser Calculation Adjustments

If my riser calculation came up with a larger fractional step or riser I'd divide that amount by the number of risers to make an adjustment so that my step risers don't vary by more than 3/8".

Example:

96" total rise / 7" riser height = 13.7 risers.

I might not want 14 steps - perhaps there's not enough horizontal run space. I could build a 13 riser stair.

That 0.7 risers could be handled like this:

0.7-fractional riser x 7-inches per riser = 4.9 inches to be gained.

I will increase my standard step riser height of 7" by 4.9 (inches to gain) / 13 risers.

4.9" / 13 risers = 0.37" per riser that I need to add if I spread the adjustment exactly evenly over all 13 riser/steps.

Or I could round that figure to 0.4" giving me a 13-steps x (0.4 - 0.37) or a 0.39" error I have to make up over several treads.

That's because the maximum allowable variation in riser height is 3/8" or 0.375" - less than my 0.39" error.

I could thus split the 0.39 over two treads with a 0.19" or about 2/10" adjustment on each of two treads. That is within acceptable uniformity limits.

At STAIR RISER SPECIFICATIONS you will find complete details about stair riser specifications and codes, including the following excerpts:

Step riser specifications riser height (<= 7.75" or in some codes <= 7.0" or in Canada <=8.25") maximum and 4 inches (102 mm) minimum. This means your stair risers should be less than or equal to 7 3/4 inches. No taller. Some codes specify slightly taller stair risers, from 8" to 8 1/4" (Canada, for example).

Step riser height uniformity (<= 3/8" variation) - this means that more than 3/8 of an inch in variation of the height of steps from one step to another is a tripping hazard.

 

When Do You Need Landings & Platforms in a Stairway?

Where space limitations require that your stairs make a single turn or where your stairs must ascend a height greater than permitted for a single run of stairs you'll need one or more stair platforms or intermediate landings. Using this example from the IRC we see that typical maximum total stair rise without a landing is 12' 7".

R311.7.3 Vertical rise.

A flight of stairs shall not have a vertical rise greater than 12 feet 7 inches (3835 mm) between floor levels or landings.

* Between landings and platforms, the vertical rise is to be measured from one landing walking surface to another.

For details of common building code specifications for stair landing dimensions and step riser and tread dimensions

see STAIR PLATFORMS & LANDINGS, ENTRY

 

How to Adjust Pre-Fab or Existing Stairs to Fit

Using pre-fab stairs - Is there an exception to the riser height variation for the very first step of the staircase?

An InspectApedia reader asked: Is there an exception to the riser height variation for the very first step of the staircase? Let me attempt to clarify the question.

I have a deck (exterior porch) for which the distance from the top of the deck to the slab which forms the footing for the set of stairs is just shy of the 5 steps within a pre-fabricated 5 step stair stringer which can be purchased at a Home Depot or Lowes, for example.

If I attach the pre-made stringer from the deck to the slab, ensuring that the top of the deck to the next stair down is the same height as the rest, then the riser height from the slab to the first stair is greater than a 3/8' variation from the rest of the riser heights by 1/8th of an inch (ie. it's 1/2 inch shorter than the rest of the stairs -

I actually need to remove a half inch from the bottom most stair of the stringer to fit). If this is a violation of code, than it means I need to cut my own customer stringer. Just verifying. Any feedback is appreciated. - Dan

Reply: no stair step riser height variation greater than 0.375 inches is allowed

Dan,

There is no exception for individual stair steps, first, bottom, top, or other. A difference in riser height can be a serious trip hazard at any location on a stairway.

Quoting from the article text above on stair and step height regularity and the amount of variation in stair step riser height that is allowed (presumably to avoid a trip hazard)

"Stair risers of uneven height - no variation greater than 0.375 inches is allowed"

How to Make Minor Adjustments to fit a factory-built stair to the specific overall stair rise

As I read your note, you have just a 1/2" error to make up between the total elevation difference between the deck surface and the ground surface if you use a pre-fabricated stair way.

If you can split the adjustment between the top and bottom stair risers by trimming the stringer top and bottom, you'll have just 1/4" or 0.25" of riser height variation (one at stair top and one at stair bottom) - thus minimizing the trip hazard risk of the uneven risers and the variation will be within standards.

Watch out: be sure to measure the height difference (deck surface to ground surface) at a projected point along a horizontal line from the edge of the deck out to the location, in horizontal distance, of the front edge of the nose of the very first or lowest step of the stairway.

That will avoid any error in calculating total stairway height due to any slope in the actual ground surface.

If you need a greater adjustment in the stair height between the ground surface and the deck surface in order to avoid having to re-cut a whole new pair of stair stringers, sometimes that can be accommodated by changing the height of the surface of the concrete or other masonry platform that many building departments and local codes require be placed as a landing at the bottom of the stairs.

Also see STAIR DIMENSIONS, WIDTH, HEIGHT

Use the 6 8 10 Rule to Square up Your Stairs Including over Une

Moved to SQUARE-UP ANY STRUCTURE USING the 6-8-10 RULE

...

---

---

ADVERTISEMENT

---

---

Reader Q&A - also see RECOMMENDED ARTICLES & FAQs

Question: how do I calculate the stair run length for these measurements? 108" rise, 11" tread depth, 8" step rise.

What is the run length needed for a rise of 108" using an 11" tread depth and 8" step rise - A.K. Debbie 11/24/2012

Reply: step by step stair calculation example

Debbie,

It's important to get comfortable with the basic math in stair calculations, and it's not too hard.

If we have to climb up 108" in height and we are going to make each step 8" tall (riser height is 8") we just divide the total rise by the step height, then adjust the step height so that we get the number of steps as a "whole number" - since we don't build fractions of a step.

1. Divide total rise by individual step rise

Divide 108 / 8 = 13.5 - so we'd need 13 1/2 steps

- which is not quite acceptable as we need to end with an even number of steps. So I would adjust the rise until the numbers came out more nicely.

2. Choose a smaller step rise to get close to a whole number of steps.

Since an 8-inch step riser height is a bit too high for safe comfortable stairway use anyway, instead of trying a still taller step to calculate the number of steps needed, I tried smaller stair rises.

I chose a sequence of numbers (7.5", 7.25", 7.125") dividing each of these into the total rise we need (108") to see how close to an exact number of steps we could achieve.

I noticed that if I set our riser height to 7.125" (about 7 1/8") we will use an even number of risers (15).

3. Make small adjustments (1/8") in successive steps as needed.

Actually it's 15.1 but once we get our riser height close to exact we can make small adjustments of say 1/8" or less in the actual riser height for individual steps to make the stairway total rise come out exactly right.

Watch out: too much variation between individual step riser heights is a trip hazard. Most codes allow up to 1/4". I find that if we keep variation to 1/8" in step riser heights nobody will notice, nor be uncomfortable.

Now with 15 risers, if I make the individual tread depth (that's the horizontal tread run distance) 11 inches, our stairway will have a run of 15 x 11 = 165" in length.

I'd check to be sure that we had proper head clearance for the stairwell and that a run of 165" doesn't run into a horizontal distance or space problem before framing the stairs

 

How do we fix old stairs whose rise won't fit in the horizontal run space?

Hi there! I have stairs outside that were built over 120 years ago and then reconfigured very badly so that the riser height varies 7cm from the lowest to highest step.

We are having them redone, but the big issue is that we have a total height of 340cm (so 20 steps of 17cm riser height will fit perfectly) but the total run is only 450cm. For a legal minimum tread depth of 25cm for each step, they simply will not fit. What do we do in this instance?

The steps kind of curve twice around a wall - it’s hard to explain - On 2022-09-07 by Huge stair problem

Reply by InspectApedia-911 (mod) - curved stairway may solve space problem

@Huge stair problem,

When you don't have enough horizontal run distance to fit the stairwell the options are

1. build a stairway that turns, with a mid-way landing

2. enlarge or move the stair opening in the upper floor to give more room for the stair run

3. I'm unclear about your stairs already curving but

consider a circular stairway if you can't fit any other stair dimension.

What are the calculations when the stair run distance is limited?

How do i calulate a stair stringer when i hav a limited run. The stairs cant fall into code i dont think the rise or the tread depth is gonna be of do i take it off the rise or the tread depth - On 2021-10-17 by Joe -

Reply by inspectapedia.com.moderator - pay attention to safety when designing stairs - and you may need an intermediate landing

@Joe,

I sure am scared about telling you how to build unsafe stairs likely to result in a fall and/or injury.

But in general terms, if the horizontal distance is the limiting factor, then both step rise height and tread depth are adjusted; you make the rise more and the tread depth less until you can fit the stairs into the available space;

You don't make the step rise so high that nobody can climb the steps.

You provide very good handrails.

You assert that the stairs are not ones in normal use that would be required to meet building stair codes.

For example, the model stair codes acknowledge that we may provide a non-compliant stair or even a ladder that gives access to special areas, such as a mechanicals loft or attic not used as living space.

 

Where do I start calculating to build stairs with a total rise of 8' 4"?

I need help in these questions......

Solve the math problems for stairs with a total rise of 8’-4’’.

1. What is the recommended starting dimension for unit rise when performing stair calculations?

2. What is the minimum number of risers in stairs?

3. What would be the largest unit rise allowed to the nearest sixteenth?

4. Using the 24-25 method, what would be the smallest unit run (tread)? - On 2021-04-06 by Urva -

Reply by (mod) - Solve the math problems for stairs with a total rise of 8’ 4"

@Urva,

Bottom line: divide the total stairway rise in inches by 7" (one riser height), then round the step riser size up or down to get an even number of steps.

Details:

1. Please take a look at the article above on this page where we address item #1.

You'll be more comfortable with the topic if you read a bit than if I just tell you start with 7"

2. I am not aware of any minimum number of risers on stairs; there will be one riser per stair tread (Plus the starter riser) IF the stairs are built with closed risers, and zero risers if the stairs are built with "open" risers as is permitted in some cases.

And if we're talking about the same thing: the tread is what you step on, and the "riser" is a vertical board or other enclosure between stair treads. I think this question is poorly-phrased.

3. There is no single right answer across the world as stair codes vary. Most get to what's considered a comfortable riser height or unit rise - explained at

STAIR RISER SPECIFICATIONS where you'll see the variation among codes

4. While this isn't exactly the same magic formula as similar ones I'm familiar with, I THINK your teacher or text is saying that 2 tread depths + 1 riser height (or variations on that) should add up to 24-25".

Take a look at the minimum recommended tread depths (again like riser height varying by code by country and city) given

at STAIR TREAD DIMENSIONS

So if we had ONE step up, from ground to an upper walking surface we would see two risers: one between the under side of the first tread and the ground, and a second between the upper surface of the tread and the under-side of the upper walking surface.

What's the largest unit rise allowed when building stairs that are easy to climb?

The total rise for stair is 8’-4’’.

What would be the largest unit rise allowed to the nearest sixteenth? - n On 2021-04-05 by Urva -

Reply by (mod) - 8 1/4"

@Urva,

Though a typical stair code says don't build steps with riser height more than 8 1/4", there won't be a "largest unit rise size" if you're building easily-climbed stairs.

Instead you start with 7" and then adjust the calculation to be exact.

You might want to try the easy procedure

at STAIR RUN CALCULATION: NUMBER STEPS

so you'll see how to do the calculation yourself any time it's needed.

Do let me know if that calculation leaves you with any questions

How do I make reinforced concrete stairs to climb 10 to 12 feet up?

I have 10 to 12 ft high and want to make rcc stairs means cemented stairs how can I make it - On 2021-01-18 by Chirag

Reply by (mod) - first pick the actual stair rise height, then we give the calculations above.

Chirag

The article above gives several methods for calculating the exact measurements for your stairs:

number of treads or risers, tread or riser height, horizontal run length of the stairs.

But you'll need to narrow down your exact total rise height.

A stair that rises "between 10 and 12 ft. " is not something anybody can build.

Please review the suggestions in the article above and then don't hesitate to ask whatever followup questions you need.

How many 7-inch tall steps do I need to a landing that's 42" above ground?

For a landing which is 42 inches from ground level, how many steps of 7 inches height should be built in standard formation - On 2021-01-14 by Ashok Viswanath

Reply by (mod) - Here's the calculation: 42" rise / 7" step riser height = 6 steps

Ashok

The procedure for calculating the exactly-correct stair riser height and number of steps is given in the article above on this page; I sure hope you'll give a look-see and do let me know if any of that is unclear.

You'll see that you start by dividing the total rise (42") by a "typical" riser height of 7" then adjust to get the exact riser height. That first division tells you the number of steps you'll need

(42/7 = 6)

What should each step and riser be so that it is at a comfortable stair angle?

@Jim, stair width is 60"

Have front porch steps need to build new steps. I know the total rise is 29" and ideally I would like the Total Run to be 41-45" What should each step and riser be so that it is at a comfortable stair angle?

Looking at Standard Trex Select Composite decking boards specs actual thickness .82" with 5.5" width 1/4" gap haven't decided on risers?

What do you recommend for steps?

risers? PVC trim? Please help - On 2020-08-09 by JIm again -

Reply by (mod) - calculating the exact stair riser height and stair run using Trex 5 1/2" wide boards for step treads

Jim,

1. Calculate the actual step riser height for your stairs:

with a 29 inch rise we figure, starting with an ideal riser height of 7" that we have 29 / 7 = 4 steps (4 x 7 =28) and to be more precise, each step will be 29 / 4 = 7.25 or 7 1/4" high.

2. Calculate the stair horizontal run distance:

4 treads, with a minimum tread depth of 11" would be 4 x 11 = 44"

Using Trex composite deck boards to build step treads, with 5 1/2" wide boards, means you could put two together to get an 11" tread, but better would be to include a small drainage gap between the boards. IMO 1/4" is too much - trapping high heeled shoes; 1/8" may not be enough if the boards swell when wet.

Suppose we use a 3/16" gap; then our actual stair treads including the tread nose formed by the outer edge of the outer board of the two will be 11 3/16" in tread depth.

That's 11.0625"

The total run then becomes very slightly longer

4 x 11.0625 = 44.25" total run.

 

How do I measure out (lay out) stairs for a total rise of 101" and a total run of 112"?

I have a stair rise of 101" and a travel distance of 112" with a maximum stair tread height in the State of GA at 7" and tread depth of 11". How do I measure that out? - On 2020-04-01 by Matthew Chamberlin

Reply by (mod) - here are the calculations

Matthew:

We start by taking a reasonable step rise, say 7 inches (we can adjust that later),

We divide the total rise by the unit or step rise.

101" total rise / 7" rise per step = 14.4

so we need a little over 14 steps up to climb that height.

Now let's design the stair using exactly 14 steps.

101" total rise / 14 steps = 7.21" rise per step. So yeah, we can build steps at that riser height - it's acceptable. (not too steep, not too shallow).

What about the horizontal distance we need?

Now that we know we want 14 steps "up", we can figure the horizontal distance as follows:

14 steps x 10" (minimum tread depth per step - noting that your building official may accept a different number) = 140 inches of horizontal travel needed for the stairs - without any intermediate landing.

So just as you can't put ten pounds of flour into an eight pound sack, you cannot build your stairs to provide a safe step height and still fit them into that 112-inch horizontal distance - not as a straight run anyway.

Worse still, 14 steps up without an intermediate landing may be prohibited by your local building department as too many steps up without a landing.

The good news - maybe - is that since you probably need an intermediate landing anyway, you can build your stairs with a landing and a turn to the upper floor - that's a way to squeeze all of that flour into a little sack.

How Many steps should my stairs be to avoid knee pain

No of steps to be provided to avoid knee pain - On 2020-03-13 by Anonymous

Reply by (mod) - Number of steps - choosing a stair step riser height avoid knee pain - use a shorter rise, 7" or less.

Anon:

You ask a great question for which there is no single right answer that works for everyone: stair dimensions and number of steps in a stairway for people with knee pain or knee and walking disability.

However for stairs that will be frequently used by such walkers, keeping the rise relatively short, 7" or less, and the number of steps between landings relatively few can make stair climbing easier. Equally important is the provision of handrails and guardrails.

Amirth

To calculate the number of stair steps between two floors you need simply the total rise - change in height - between floors, divided by a desirable step rise - say 7" - then round or adjust the actual rise so that you have the same rise on every step and that the total rise is accomplished. Details are in the article above on this page.

 

Calculate the stair steps to a first floor measuring tread 13" and depth of 6"

How to. Calculate the stair steps to a first floor measuring tread 13" and depth of 6" - On 2020-03-13 by Amirtheswaran -

Reply by (mod)

Amirth

To calculate the number of stair steps between two floors you need simply the total rise - change in height - between floors, divided by a desirable step rise - say 7"

- then round or adjust the actual rise so that you have the same rise on every step and that the total rise is accomplished. Details are in the article above on this page.

...

Continue reading at STAIR DIMENSIONS, WIDTH, HEIGHT or select a topic from the closely-related articles below, or see the complete ARTICLE INDEX.

Or see STAIR RISE & RUN CALCULATION FAQs - questions and answers posted at the end of this article.

Or see these

Recommended Articles

• 6-8-10 RULE to SQUARE UP ANY STRUCTURE - use this trick to square up your stairs or any other structure
• CALCULATE stair tread depth or riser height from stairway slope in degrees
• FRAMING TRIANGLES & CALCULATIONS
• LANDSCAPE TIE STAIR CALCULATIONS - build stairs to a specified total rise AND total horizontal run distance
• ROOF SLOPE CALCULATIONS - mathematics of calculating stair or roof slope, angle, pitch, rise, run, + examples of using trigonometric functions eg. tangent
• SQUARE PLUMB & LEVEL A STRUCTURE
• STAIR BUILDING RULES of THUMB
• STAIR ANGLE & SLOPE - Stairway Slope or Angle & Stair Tread Slope Allowed
• STAIR CONSTRUCTION, LOW ANGLE SLOPE
• STAIR CONSTRUCTION, SPECIFIC ANGLE or SLOPE - build stairs to a pre-set angle or slope
• STAIR CONSTRUCTION, SPECIFIC TOTAL RISE & RUN - using landscape ties as example
• STAIR DESIGNS for UNEVEN / SLOPED SURFACES
• STAIR DIMENSIONS, IDEAL
• STAIR CONSTRUCTION, LOW ANGLE % SLOPE - Find the Percent Slope & Angle of Low-Rise Stairway
• STAIR RISE & RUN CALCULATIONS - home
• STAIR PLATFORMS & LANDINGS, ENTRY - when do we need an intermediate stair landing or platform? Where to measure.
• STAIR RISE & RUN GEOMETRY & CALCULATIONS - for uneven surfaces
• STAIR RISER SPECIFICATIONS

Suggested citation for this web page

STAIR RISE & RUN CALCULATIONS at InspectApedia.com - online encyclopedia of building & environmental inspection, testing, diagnosis, repair, & problem prevention advice.

Or see this

INDEX to RELATED ARTICLES: ARTICLE INDEX to STAIRS RAILINGS LANDINGS RAMPS

Or use the SEARCH BOX found below to Ask a Question or Search InspectApedia

Ask a Question or Search InspectApedia

Try the search box just below, or if you prefer, post a question or comment in the Comments box below and we will respond promptly.

Note: appearance of your Comment below may be delayed: if your comment contains an image, photograph, web link, or text that looks to the software as if it might be a web link, your posting will appear after it has been approved by a moderator. Apologies for the delay.

Only one image can be added per comment but you can post as many comments, and therefore images, as you like.
You will not receive a notification when a response to your question has been posted.
Please bookmark this page to make it easy for you to check back for our response.
Our Comment Box is provided by Countable Web Productions countable.ca

Citations & References

In addition to any citations in the article above, a full list is available on request.

---

ADVERTISEMENT

---