Roof Measurements from the Ground Using a Folding Ruler
Roof Measurements from the Ground Using a Folding Ruler
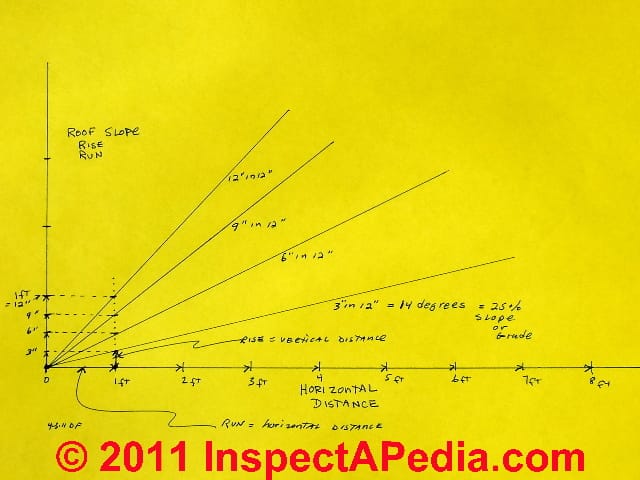
Slope, Rise, Run, Area
measurements using a folding carpenter's rule
- POST a QUESTION or COMMENT about types of roofing materials, installation, inspection, diagnosis, repair, maintenance, & warranties
Carpenter's folding rule for measuring roof slope:
How to use a folding rule to measure angles, roof slope, pitch, area and other dimensions: here we show how to use a carpenter's folding ruler to obtain the slope and other dimensions of a roof.
Simple observations made from the ground can give a good approximation of the roof slope. In turn number along with a table we provide, or with a simple calculator, it is easy to figure any measurement of a roof: rise, slope, area, pitch etc.
Although you do not need to understand Tangents, we include an explanation and examples of how to use the tangent TAN and inverse tangent to TAN-1 find roof slope in degrees, roof rise, run, etc.
Roof measurement methods: these articles explain various methods for measuring all roof data: roof slope or pitch, rise, run, area, and other features. This article series gives clear examples just about every possible way to figure out any or all roof dimensions and measurements expressing the roof area, width, length, slope, rise, run, and unit rise in inches per foot.
InspectAPedia tolerates no conflicts of interest. We have no relationship with advertisers, products, or services discussed at this website.
- Daniel Friedman, Publisher/Editor/Author - See WHO ARE WE?
How to Measure Roof Slope From the Ground Using a Folding Carpenter's Rule
As you've see from out other roof measurement examples beginning at ROOF MEASUREMENTS, knowing the roof slope is really handy as something we can measure up close but also from a distance, obtaining a number that plugs into simple formulas for roof area too.
What if the roof is inaccessible from outdoors, and there is no access to the building interior (i.e. its attic) so we cannot make direct roof slope measurements, but we still need to know its slope?
You need a simple folding carpenter's rule.
It helps to have a steady hand and to read the instructions on exactly where to read the inches on the bottom scale in the folding rule triangle that we show at left.
Use a Folding Rule to Get Roof Angle or Slope: Method 1 - align the folding ruler segments to match the roof slope at the building gable end
You need: a folding carpenter's rule and a second ruler, tape measure, or carpenter's rule. To be fancy and more precise you can also use a carpenter's 4 ft. level as we will describe.
Stand about 30 feet away from the gable end of the building where you can see the triangle formed by the front and rear roof slope edges.
Match the folding ruler first two segments to the roof slopes:
Open the ruler to form three segments as shown in our photograph above. The beginning segment (held on on your left) and the second segment (held on your right) are held up and adjusted to exactly match the slope of the roof. The 3rd and 4th segments of the folding ruler are held horizontal or parallel to the ground. (Or parallel to your 4 ft. level if you like.)
Hold this assembly level and check that the angle formed by ruler segments1 and 2 match the roof slopes.
I place the roof inside the triangle formed by my folding ruler.
Set the folding ruler bottom segments horizontal:
bring up the horizontal segments of the folding carpenter's rule to a horizontal position - level with the building. In fact, in my photo (above left) you can see a mistake - the left end of the first folding ruler segment projects a bit below the horizontal bottom of my triangle - excuse me but taking the photo while holding this stuff was a bit tricky.
You get the idea. In a perfect world the bottom corner of the first ruler segment should be in the center of the horizontal segment, not at the top, not at the bottom.
We explain this detail below at FOLDING RULE CALIBRATION. But it's not critical because we read the horizontal ruler scale along the top edge of the horizontal portion.
Read the number of inches on top edge of the bottom segment of the folding ruler where ruler segment 1 bottom corner crosses the lower horizontal segment.
This number will be along the inches scale somewhere between 15 1/2" (which would be a single slope on the right and a 90 degree slope on the left) and 24" (which would be a dead-flat roof).
The reasons we use the top edge of the bottom segment for our folding ruler roof-slope readings are two:
That is how we measured and calibrated our Folding Ruler to Roof Slope Table below.
We are aligning the actual building roof slopes with the inside of our folding ruler triangle. To be consistent we make our horizontal length measurement also inside the triangle formed by our folding ruler.
One can make an equally accurate folding ruler scale using inch-marks where the bottom-most corner of the left-hand sloping ruler segment touches the scale, but I find that that location is hard to keep consistent as the roof angles vary.
To convert the inches read along the folding rule, find the approximate roof slope in the folding ruler conversion table
at FOLDING RULER to SLOPE DATA TABLE - found just below. There we provide the necessary table converting folding ruler inch-scale to roof slope below.
In the table you will see data for two basic roof shapes: a single slope or shed type roof, and a double slope or conventional gable type roof.
When reading a folding ruler triangle opened to match two roof slopes (left and right seen from the building gable-end) and for anything but a vertical left slope or a dead flat roof, we are going to read a number typically somewhere between the 20-inch ruler mark and the 24-inch ruler mark. You will see that data in the Gable Roof column second from left in our table.
If we are reading a folding ruler triangle for a shed roof, that is a single slope, the other folding ruler segment will be set to vertical or 90 degrees and will cross the horizontal segment giving an inches-measurement. You will see that data in the Shed Roof or left-most column of our table.
To obtain roof area we can use slope or tangent number to obtain the actual dimension of the sloping roof edge - the roof width. That is, if we know the angle and the length of a single side of a right triangle we can calculate the lengths of the other two sides and thus we can obtain the total roof area too.
For a table of tangent values
see TANGENTS TABLE
also see ROOF SLOPE CALCULATIONS
Table of Conversion Numbers: Folding Ruler Scale Translates to Roof Slope
Notes to the table above
1. These horizontal ruler scale numbers were actually measured using a protractor. For example, 19 7/8" on the scale was calibrated at 45 deg. using the procedure explained at FOLDING RULER CALIBRATION. All of these triangles are right triangles.
2. For a two-slope gable roof one cannot just double the single slope shed roof horizontal distance because as soon as we un-bend the vertical ruler segment used for the 90 deg. line for a shed roof we see that the lengths of the sloping roof segments change continuously as we change the angle.
That's the effect of a center-hinged folding rule and the use of either the outer or inner edge of the ruler to sight (in the field) or measure (with a protractor) roof slopes or angles.
We would have to use a clear folding rule that sports a line running through the center of the rule's width as our alignment. For this reason, carefully setting the left and right gable roof angles with a protractor and noting the horizontal ruler scale cross-point along its top edge seems the best approach.
3. Since two of our roof angles are 60 deg. we know that all 3 angles are 60 deg and this is an equilateral triangle because triangle sides a + b + c = 180 deg.
4. Since two of our roof angles are 45 deg. we know that the third angle, the two slopes meeting at the ridge, or the apex of the triangle, will be at 90 deg. Because triangle sides a + b + c = 180 deg.
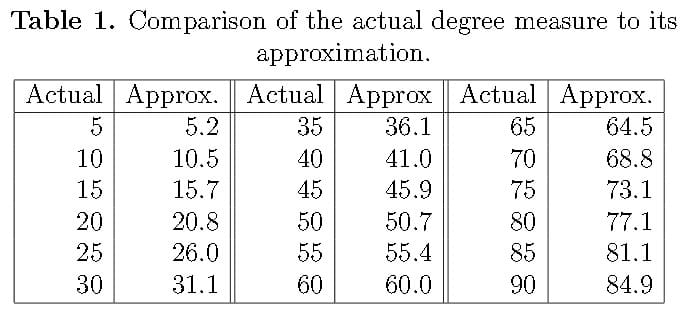
5. Approximations
6. This approach works using a folding rule until the roof slopes get very low. Then it is impossible to read the scale on the inner edge of the ruler-formed-triangle.
7. Tangent = Rise / Run also allows us to obtain roof slopes in degrees, and vice versa.
see TANGENTS TABLE
The Tan value for a 55 deg slope roof = Tan ( 55) = 1.43
The inches of run for 12-inch rise for a 55 deg slope roof is calculated as 1.43 = 12 / run or Run = 12 * 1.43 = 17.3"
The inverse Tan-1 function can convert a Tan value back into degrees of roof slope.
Tan-1 (1.43) = 55 deg. and wonderfully, Tan-1 (1.00) = 45 deg.
Since Tan is a simple ratio of unit Rise / unit Run, we note that we can quickly convert a roof slope in degrees into the number of inches of rise per 12" of run as follows, using a 55 deg. slope as example:
Tan (55) = 1.43
Since 1.43 = rise / run we can use simple algebra to write:
1.43 x 12" run = 17.16" of rise per 12" of run
Calculations & Formulas for finding Rise, Run, % Slope of a Roof or other sloping surface
For a complete guide to calculating any roof data you need from whatever numbers or data you have, please see ROOF CALCULATIONS SUMMARY.
There we explain how we obtain the total roof area, number of squares of roofing materials to order, roof pitch or slope, and other helpful data.
Below are a couple of details that I include to warn about messing with folding rulers.
Rise in inches = Tan x Unit-Run" = Unit Rise" for any slope expressed in degrees, use the Tangent value to calculate rise for a 12-inch run:
Watch out: for cases such as our folding ruler triangles, you are not working with a fixed horizontal unit run of 12-inches, nor an exact 6-inch roof slope length (hypotenuse of the triangle).
You will observe that the actual length of a folding ruler segment bent to follow a roof slope will lengthen as the slope is steeper and shorten as the slope is less steep. This is because the hinge point of the ruler segment is fixed and the edge of the sloping ruler segment moves closer to or further from the top of the horizontal ruler segment as you fold the ruler.
Slope in degrees = Tan * (Rise / Run)
Grade%: %Grade = Rise / Run x 100 but be sure Rise & Run are expressed in same units)
Methods of Folding Rule Inch-Scale Calibration to Read Roof Slopes & Angles
At FOLDING RULER ROOF SLOPE CALIBRATION we describe some fun approaches can be sued to calibrate the folding rule inch-readings that give roof slope in the procedure described above.
We can set the slope of folding ruler segments using a protractor and note where the folding ruler crosses the horizontal ruler scale: easy but you have to work with care, or we can calculate the number of inches of horizontal run for various triangles all of whom have a 6-inch hypotenuse but whose angle and thus horizontal run length change, using trigonometry.
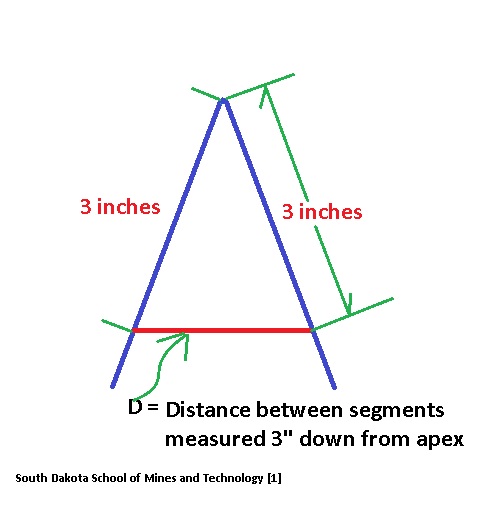
Use a Folding Rule to Get Roof Angle or Slope: Method 2 - the 3-inch rule
Following the same procedure as used above, align the folding ruler so that its first two segments exactly match the roof front and rear slopes. But the calculation approach is a bit different and really neat.
The original 3-inch rule discussed by the South Dakota School of Mines and Technology [1] was documented as applying to acute angles (angles of 90 degrees and less) with some suggestions on how that approach might be used for obtuse angles such as found on most building roofs.
Here we elaborate that procedure to apply to building roofs that will normally be much less steep - properly, obtuse angles. We start by explaining the acute angle measurement and then explain how to make obtuse angle measurements using the folding ruler.
Acute angle measurement using a folding ruler
Using a folding carpenter's rule calibrated in inches, set the first and second segments of the rule to match the roof slopes while standing at the gable end of the building and sighting across the folding rule, holding it in alignment with the roof edges.
Without changing the angle to which the ruler segments are bent, use a second straight ruler or tape (or with help from an assistant) to measure the distance between a point that is exactly 3 inches down from the apex of the triangle, measuring along the inside edge of the ruler - mark or note this point on both the left and right ruler segments.
For consistency I align the inside of the folding rule to the roof edges and make all measurements along the inside edge of the folding carpenter's rule segments.
Now using a ruler or tape measure, measure the horizontal distance between those two 3-inch marks.
Multiply that distance by 20.
This approach works for angles up to 90 degrees. The number will be the approximate slope of the roof expressed in degrees as you will read in the table just below.
Obtuse angle measurement using a folding ruler
To measure an obtuse angle (which is normally the case for roof angles) let ruler segment 1 follow the roof slope, set segment 2 at 90 degrees to ruler segments 3-4, hold segments 3-4 level, and re-check that segment 1 still follows the roof slope. The obtuse angle is then split in two, we use the same 3-inch rule and table as before, and add the two angles together to get the obtuse angle in degrees.
As the original author explained:
This method can be easily applied to approximate an obtuse angle as well. For example, one can approximate the corresponding supplementary angle and subtract this result from 180 ± .
Alternatively, one can measure the angle's excess past 90 ± using the end of the ruler as a convenient right angle, or if your ruler happens to be damaged from years of use (or disuse!), divide the angle into two acute angles and add their approximations. - South Dakota School of Mines and Technology [1]
This procedure was originated by Tor Bertinm a student at the South Dakota School of Mines and Technology, SDSM&T and is nicely documented by an author who modestly omitted his name, but posted a helpful and detailed analysis of this approach at the web link given below. [Click to enlarge the table or any other image at InspectApedia.com]
- "How to Measure Angles with a Ruler", South Dakota School of Mines and Technology, Website: http://www.mcs.sdsmt.edu, http://www.mcs.sdsmt.edu/tkowalsk/portfolio/downloads/pub_HowToMeasureAngles.pdf retrieved 10/26/2013, copy on file.
...
Continue reading at FOLDING RULER ROOF SLOPE CALIBRATION or select a topic from the closely-related articles below, or see the complete ARTICLE INDEX.
Or see these
Recommended Articles
- 6-8-10 RULE to SQUARE UP ANY STRUCTURE
- ANGLE FINDER LEVEL - set this tool on any slope and it'll tell you the angle
- ARCTANGENT CALCULATES ROOF / STAIR ANGLE
- CALCULATE RISE & RUN from SLOPE
- SQUARE PLUMB & LEVEL A STRUCTURE
- FOLDING RULER ROOF SLOPE CALIBRATION
- FRAMING SQUARE USER'S GUIDE
- FRAMING TRIANGLES & CALCULATIONS
- FROGS HEAD SLOPE MEASUREMENT
- HOPPUS MEASURER
- PRINTABLE PROTRACTOR [Image file]
- RAMP SLOPE or PITCH
- ROOF MEASUREMENTS
- ROOF SLOPE CALCULATIONS
- ROOF SLOPE DEFINITIONS
- ROOF SLOPE TABLE, TYPES, WALKABILITY
- STAIR RISE & RUN CALCULATIONS
- FRAMING TRIANGLES & CALCULATIONS
Suggested citation for this web page
ROOF MEASURE by FOLDING RULE at InspectApedia.com - online encyclopedia of building & environmental inspection, testing, diagnosis, repair, & problem prevention advice.
Or see this
INDEX to RELATED ARTICLES: ARTICLE INDEX to BUILDING ROOFING
Or use the SEARCH BOX found below to Ask a Question or Search InspectApedia
Ask a Question or Search InspectApedia
Try the search box just below, or if you prefer, post a question or comment in the Comments box below and we will respond promptly.
Search the InspectApedia website
Note: appearance of your Comment below may be delayed: if your comment contains an image, photograph, web link, or text that looks to the software as if it might be a web link, your posting will appear after it has been approved by a moderator. Apologies for the delay.
Only one image can be added per comment but you can post as many comments, and therefore images, as you like.
You will not receive a notification when a response to your question has been posted.
Please bookmark this page to make it easy for you to check back for our response.
IF above you see "Comment Form is loading comments..." then COMMENT BOX - countable.ca / bawkbox.com IS NOT WORKING.
In any case you are welcome to send an email directly to us at InspectApedia.com at editor@inspectApedia.com
We'll reply to you directly. Please help us help you by noting, in your email, the URL of the InspectApedia page where you wanted to comment.
Citations & References
In addition to any citations in the article above, a full list is available on request.
- [1] "How to Measure Angles with a Ruler", South Dakota School of Mines and Technology, Website: http://www.mcs.sdsmt.edu, http://www.mcs.sdsmt.edu/tkowalsk/portfolio/downloads/pub_HowToMeasureAngles.pdf retrieved 10/26/2013, copy on file.
- ARMA - Asphalt Roofing Manufacturer's Association - Asphalt Roofing Manufacturer's Association - https://www.asphaltroofing.org/
750 National Press Building, 529 14th Street, NW, Washington, DC 20045, Tel: 202 / 207-0917 - NRCA - National Roofing Contractors Association - Website: www.nrca.net 10255 W. Higgins Road, Suite 600, Rosemont, IL 60018-5607, Tel: (847) 299-9070 Fax: (847) 299-1183
- copy on file as /roof/Roofing_Historic_NPS .pdf Roofing for Historic buildings", Sarah M. Sweetser, Preservation Brief 4, Technical Preservation Services, National Park Service, U.S. Department of the Interior, web search 9./29.10, original source:
http://www.nps.gov/history/hps/tps/briefs/brief04.htm - Building Pathology, Deterioration, Diagnostics, and Intervention, Samuel Y. Harris, P.E., AIA, Esq., ISBN 0-471-33172-4, John Wiley & Sons, 2001 [General building science-DF] ISBN-10: 0471331724 ISBN-13: 978-0471331728
- Building Pathology: Principles and Practice, David Watt, Wiley-Blackwell; 2 edition (March 7, 2008) ISBN-10: 1405161035 ISBN-13: 978-1405161039
- Handbook of Building Crafts in Conservation, Jack Bower, Ed., Van Nostrand Reinhold Company, NY 1981 ISBN 0-442-2135-3 Library of Congress Catalog Card Nr. 81-50643.
- Historic Preservation Technology: A Primer, Robert A. Young, Wiley (March 21, 2008) ISBN-10: 0471788368 ISBN-13: 978-0471788362
- In addition to citations & references found in this article, see the research citations given at the end of the related articles found at our suggested
CONTINUE READING or RECOMMENDED ARTICLES.
- Carson, Dunlop & Associates Ltd., 120 Carlton Street Suite 407, Toronto ON M5A 4K2. Tel: (416) 964-9415 1-800-268-7070 Email: info@carsondunlop.com. Alan Carson is a past president of ASHI, the American Society of Home Inspectors.
Thanks to Alan Carson and Bob Dunlop, for permission for InspectAPedia to use text excerpts from The HOME REFERENCE BOOK - the Encyclopedia of Homes and to use illustrations from The ILLUSTRATED HOME .
Carson Dunlop Associates provides extensive home inspection education and report writing material. In gratitude we provide links to tsome Carson Dunlop Associates products and services.