Water tank pressure, temperature & volume calculations:

This article describes Water Tank Pressure Calculations - the effects of temperature, air charge, tank size, pump pressure settings on water system performance, using Boyle's Law, Charles' Law, and the Combined Gas Law in a building water supply system where a private well is the water source.

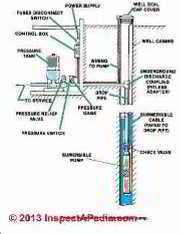
We continue to explain why a pure application of these laws is insufficient to account for water pressure tank behaviour, and we pose a "water pressure tank law" that fits practical applications in buildings. The illustration at page top is courtesy of Carson Dunlop Associates, Inc. in Toronto.

The Effects of Ambient Air Temperature on Water Tank Performance

This article examines the effects of ambient air temperature changes, water temperatures, and the water tank air charge or tank pressures on water pump and water tank operations and performance.

If your water pump, well, or water tank don't seem to be working right, this article gives some useful and basic underlying theory that might help understand what's going on.

Article Series Contents

• WATER TANK PRESSURE CALCULATIONS
  • HOW A WATER PRESSURE TANK WORKS - Using the gas laws to calculate the effects of a change in volume, pressure, or temperature of any gas in a closed container.
  • BOYLE's LAW
  • WATER VOLUME DRAW DOWN during a typical water pump and water tank operating cycle?
  • CHARLES' LAW
  • COMBINED GAS LAW
  • WATER PRESSURE TANK LAW: why Boyle's, Charle's, and the Combined Gas Law are Wrong about Water Tank Air and Water Pressures
  • WATER TEMPERATURES Control In-Tank Pressures Along With the Water Pump Switch
  • LETTING AIR OUT of a WATER TANKcould Improve Water Pump Short Cycling
  • GAS LAWS & CONSTANTSof interest to people with home water pumps, water tanks, & maybe wells

The effects of temperature on water pressure tank volume and water delivery are very small and are generally ignored in most calculations regarding the behavior of water pressure tanks. We visited this topic and documented the underlying principles and calculations at the request of several readers.

The amount of usable water volume that is delivered by a water pressure tank is essentially equal to the volume of expanding air inside the tank while water is leaving the tank. (Water is not very compressible so all of the volume change is due to the air pressure.) Our discussion

of BOYLE's LAW explains that P₁V₁ = P₂V₂

or stating Boyle's gas law in plain English, that the multiple of Pressure x Volume remains constant.

In other words, as water leaves the tank and thus air pressure inside the water tank decreases, the volume of air expanding inside the tank increases accordingly.

So if P₁V₁ represents the starting pressure and volume, P₂V₂ will represent the ending pressure and volume, and while the P's and V's themselves change, the multiple of P₁V₁ will always equal P₂V₂ (unless air also escapes from the tank along with water).

A reader wrote that letting air OUT of her water tank improved the pump performance, leading her to pose that the tank had previously contained too much air volume (or pressure) due to changes in ambient air around the tank in warm weather.

Let's consider what happens to air pressure in a water tank under varying conditions. While experts agree that the effects of temperature on the operating cycle of a water pressure tank are generally negligible, we agreed to look at the question more technically and in detail.

How a Home Water Tank Works

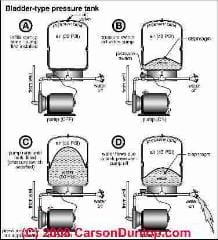A bladder-type water pressure tank has the air pumped into the tank, usually from the top at a schrader valve, and that air never escapes unless the tank or its water-bladder has a leak.

This tank pre-charge is set at the factory but might be adjusted by a plumber depending on the operating pressure range of a particular water pump and control.

The volume of the water tank is fixed. Here I'm using an idealized 30 gallon tank.

As water is sent by the pump into the bladder in the tank bottom, the bladder swells and the air above it in the tank is compressed. The volume occupied by the air decreases.

The pressure of the air increases (up to the cut-off pressure set by the pump control). The volume occupied by the water (in the bladder) increases by the same amount as the air volume decreases.

Sketch courtesy of Carson Dunlop Associates, a Toronto home inspection, education & report writing tool company [ carsondunlop.com ].

How Much Does Water Tank Air Volume Vary?

For our theoretical, simplified water tank and treating air as an ideal gas:

Suppose we have a water tank that is 30 gallons of cubic space and our pump control is set to cut-in at 33 psi And cut out at 50 psi.

Suppose inside the tank is a water bladder that can hold between 0 gallons and 10 gallons of water. I am cheating a little on choice of these numbers just to make the math easy as you'll see below.

30 gallons (total tank size) is 4 cubic feet of space. (http://www.western-water.com/Acre-Foot_formula.htm)

With the water bladder full we have:

• 20 gallons of air at 50 psi and occupying 2.67 cubic feet. The water pump has reached its cut-off pressure.
• 10 gallons of water in the tank is being pressed-on with 50 psi of force and occupying 1.33 cubic feet. This pressure is what sends water out of the tank and through the pipes to the shower.

Boyles Law Describes How Water Tank Air Volume Changes With Pump Pressure

We can re-examine the calculation of variation in water tank air volume in more detail

using BOYLE's LAW.

Boyles Law:   P₁V₁ = P₂V₂  at constant temperature tells us how the volume of a gas changes with changes in pressure, or vice versa, how the pressure of gas changes if we change its volume.

Turning on the water somewhere in the system, we run all of the water out of the tank. (This is not what happens in normal water pressure tank operation. Normally the water pump comes on before all of the water has been pushed out of the water tank. We are using all of the water in this example for simplicity and to describe the absolute maximum amount of water that could be taken out of a water pressure tank.

What happens in the water tank as we run out its water completely? The water volume in the tank goes from 10 gallons to zero. The air volume in the tank goes from 20 gallons to 30 gallons. (Or if you prefer we can convert all of these gallons to cu. ft. - the equations don't care)

What happens to the air pressure during this change? We can work in gallons or cu. ft. of volume.

20g x 50 psi = 30g x ? PSI solving for PSI = (20x50)/30 = 33 psi

Now in the tank we have 30 gallons of air (or 4 cubic feet of air) at 33 psi. and we have 0 gallons of water with a tank bottom pressure at the water outlet = the air pressure in the tank = 33 psi.

At this point the pump comes back on and pushes water back into the tank.

As water enters the tank bladder it expands the bladder and takes up room in the tank, compressing the air in the tank from 33 psi. back up to 50 psi (the pump cut-off point) and back to our original 20 gallons of air at 50 psi and occupying 2.67 cubic feet and 10 gallons of water being pressed-on with 50 psi of force and occupying 1.33 cubic feet.

What happens when we use absolute pressures and then repeat the Boyle's Law calculation performed above:

For a water tank whose pump turns on at gauge pressure of 30 psi and off at gauge pressure of 50 psi, the absolute pressures (adding 14.7 psi for one atmosphere at sea level) will be 44.7 psi and 64.7 psi respectively.

Using our example of pretending that we can take all of the water out of the water tank (0 or now 14.7 psi when the tank is "empty" of water) and that we then pump water back in to a pressure of 50 psi, and using a water tank with a 10 gallon internal volume which will be occupied by some volume of water and air when the pump cycles off:

Tank Volume = 10 gallons = Water Volume + Air Volume

Tank Volume = 10 gallons = 0 gals Water + 10 gals Air (at 0 gauge pressure or 14.7 absolute pressure) when the tank is empty

Let's now pump in water until our water tank pressure reaches 50 psi (gauge) or 64.7 psi (absolute pressure)

Tank Volume = 10 gallons = W gals Water + A gals Air

Using basic algebra, W gals Water = 10 gallons - A gals Air

The air volume in the tank has changed to 10 gallons at 14.7 psi to A gallons at 50 psi.

Using P₁V₁ = P₂V₂, we have (14.7 psi x 10 gals) = (50 psi x A gals) (just looking at the change in air volume)

(14.7 x 10) / 50 = A gals of Air or 2.94 gallons. Our air, compressed from 10 gallons at 14.7 psi to the new pressure of 50 psi will now occupy just about 3 gallons of volume.

Finally! How much space will be occupied by water in our 10 gallon tank?

10 gallons of air compressed down to 3 gallons of air, letting in (10-3) or 7 gallons of water. We have 7 gallons of water in the 10 gallon water tank when the pump shut off at 50 psi.

Now let's adjust our calculations to account for the normal operating range of a water pressure tank and water pump that turns on at 20 psi and off at 50 psi.:

At 50 psi (gauge) in our 10 gallon water tank we have 7 gallons of water and 3 gallons of air.

At 0 psi (gauge) in our 10 gallon water tank we have 0 gallons of water and 10 gallons of air (at 0 gauge or 14.7 psi absolute pressure)

At 20 psi what are our water and air volumes?

Air: (14.7 psi x 10 g) = (20 psi x A gals) or (14.7 x 10)/20 = 7.35 gals of air which leaves (10 - 7.35) = 2.65 gals of water. So at 20 psi we have 7.35 gallons of air and 2.65 gallons of water in the pressure tank, and at this point the pump comes back on to send in more water.

So what is the draw down volume of water in a 20-50 psi 10 gallon water pressure tank?

We subtract the 20 psi water volume (2.65) from the 50 psi water volume (7.00) and we get (7.00 - 2.65 = 4.35).

So the draw down volume of water in a 10 gallon water pressure tank operating between 20 psi and 50 psi will be just 4.35 gallons!

What is the actual water volume draw down during a typical water pump and water tank operating cycle?

One can conclude a few useful things from this calculation

• A 10 gallon water pressure tank that starts fully empty and is pumped up to about 50 psi will contain about 3 gallons of air and 7 gallons of water
• The water tank in normal operation does not draw down to 0 gauge pressure before the pump comes on. Rather it draws down to 20 psi when the pump comes on.
• A water pressure tank with a total volume of 10 gallons and operating between 20 psi and 50 psi of pressure will have a draw down water volume of just 4.35 gallons of water.
• A typical kitchen water faucet runs between 3 gpm and 5 gpm (varying as the water pressure in the system varies as the water pump cycles on and off), so we can expect to run the water at the tap for about a minute before the pump will come on with this theoretical water tank.
• Because the pressure drops as the water tank empties and then increases as the water pump comes back on, the water pressure at a faucet or other plumbing fixture will vary between the pump cut-in pressure (typically 20 psi or 30 psi) and the pump cut out cycle (typically 40 psi to 50 psi).

Charle's Law Describes How Water Tank Air Pressure Changes With Shifts in Air Temperature in the Water Tank

What about the effects of changes in ambient temperature around a water storage/pressure tank? Suppose we wonder if seasonal temperature changes might cause important changes in in-water-tank pressure. For simplicity we'll work with a fixed volume full tank of just air. We'll change the temperature of the tank and its air from 60 deg.F. to 90 deg.F.

As most people would guess from practical experience, raising the temperature of a container of air while keeping the container size fixed will increase the pressure of air in the container.

If we raise the temperature of a cubic foot of air, the air will want to occupy a larger volume.

30gal of air (or 4 cu. ft.) of air at 33 psi and at 60 degF is changed to 90 degF (by the warming ambient air) while the container size is kept constant.

4cu.ft./520degF = NEWCUFT/550degF

or NEWCUFT = 4cu.ft./(550degF/520degF) or about 4.2 cu. ft.

The above is corrected from the following older, incorrect formula, thanks to Mr. Slover cited just below.

Charles would say: 4cu.ft./60degF = NEWCUFT/90degF or 0.066 = NEWCUFT/90 0.066 x 90 = NEWCUFT or about 6 cu. ft.

Reader Comment: using Charles' Law more-accurately

One of the sections that describes the temperature effect on tank pressure using Charles’ Law has a few problems. The paragraphs in question are

30gal of air (or 4 cu. ft.) of air at 33 psi and at 60 degF is changed to 90 degF (by the warming ambient air) while the container size is kept constant.

Charles would say: 4cu.ft./60degF = NEWCUFT/90degF or 0.066 = NEWCUFT/90 0.066 x 90 = NEWCUFT or about 6 cu. ft.

1. Since by the second paragraph expansion takes place, then the first paragraph’s constraint of constant container size should be removed from the first. This is consistent with the next section when it is shown that if you constrain the “container size,” pressure must rise.

2. The expansion calculated uses degrees F. It should use absolute (degrees Rankine). Alternatively, you can use Kelvin as you did in the following section. (Incidentally unlike all other temperature scales, Kelvin is not preceded by “degrees.” It is the SI unit for temperature and degrees is understood.)

3. Therefore, using degrees R your paragraph would be

Charles would say: 4cu.ft./520degF = NEWCUFT/550degF

or NEWCUFT = 4cu.ft./(550degF/520degF) or about 4.2 cu. ft.

Or in K

Charles would say: 4cu.ft./288K = NEWCUFT/305K

or NEWCUFT = 4cu.ft./(305K/288K) or about 4.2 cu. ft.

4. The temperature ratio is the same as used in the next section.

- William Slover, 2020/09/14

Moderator reply:

Thank you for taking time to write about Charles' Law and to suggest editing for accuracy. We add your comments in this article in correction/ clarification.

We can't of course actually remove the constraint of the container size in that the physical dimensions and thus the total volume of a water pressure tank is fixed.

Details about Charles' Law are

at CHARLES' LAW

The Combined Gas Law Helps Explain What Happens Inside of a Water Tank

But inside of our water tank the total space available for air is fixed by the physical size of the tank itself. If we're talking about air inside a water tank, the volume taken up by the air can't get bigger than the tank itself.

We need to look at pressure and temperature simultaneously using the Combined Gas Law:   P₁V₁/T₁ = P₂V₂/T₂  

• Starting Formula: (33 psi X 4 cu. ft.) / 60degF = (NEWPSI X 4 cu. ft.) / 90degF
• Corrected (for temperature) Combined Gas Law Formula: (33 psi X 4 cu. ft.) / 288 degK = (NEWPSI x 4 cu. ft.) / 305 degK
• 132 / 288 = (NEWPSI x 4) / 305
• 35 = NEWPSI - so we went from 33 psi to 35 psi when we increased the temperature of the air in the tank from 60 degF. to 90 degF.
• (35-33)/33 = .06 or in other words, we see about a 6% increase in pressure in the water tank when the temperature changes from 60 degF. to 90 deg.F.

Details of these calculations are shown

at COMBINED GAS LAW

Water Tank Pressure & Volume Law

All of These Laws, Boyle's, Charle's, and the Combined Gas Law, are Wrong about Water Tank Air and Water Pressures

In THEORY our hypothesis that warming weather could cause water tank and pump short cycling since if we heated up the air in the tank it would occupy more and more space until there was little or no water in the tank. The pump would have to keep turning on and off when we were running the water.

But this is NOT the case when we consider that we're letting water back into the tank along with our air in there. Our theory is wrong because we forgot something: the air in the tank is cooled by the incoming water.

In a real, in-use water tank, the incoming water from almost any water supply is well below ambient air temperature, and from a well the water is often sitting around underground at 40 degF. which would easily cool the water tank and thus the air it contains.

This is why in humid climates we see condensate on the outside of the tank.

The incoming water is cooling off the water tank! The water would have to sit idly in the water tank for a long time before the tank would warm up to ambient air temperatures outside the tank.

So we have two explanations for the absence of much effect on water pressure tank performance when the ambient temperatures around the water tank change: the combined gas laws showed about a 6% pressure change in a typical water pressure tank with a 30 degF. temperature increase in the tank, and when we add the cooling effects of cool water entering the tank in most environments this pressure change is reduced further.

Only in locations where the water entering a water pressure tank is at high temperatures would the water temperature affect tank pressures noticeably.

(We might see these effects in some parts of the Southwestern U.S. where groundwater or municipal water temperatures are high or where a well is tapping thermal springs.

Water Temperature Effect on Water Tank Operation

Incoming Water Temperatures Control In-Tank Pressures Along With the Water Pump Switch, initial air volume & pressure in the water tank

In conclusion and despite the help from Boyle and Charles and the Combined Gas Law, the cooling effect of low-temperature incoming water which is almost always well below ambient air temperature will offset any the effects of seasonal changes of air temperature around the water tank (except maybe if the pressure tank is in hot direct sunlight which I'll skip for now).

In fact, if anything, the air in the water tank is cooled to below room temperature by the incoming water, which in turn would tend to lower, not raise, the air pressure in the system.

Only if the incoming water were at or above ambient air temperatures would we be likely to see an effect on water pump and tank behavior from seasonal ambient air temperature changes.

Letting Air Out of a Water Tank

Since We Broke the Gas Laws, What Explains Why Letting Air OUT of a Water Tank could Improve Water Pump Short Cycling?

SO the most likely explanation for the improvement that we saw when you released air from your captive-air water pressure tank is that

• Someone added too much air to the tank, perhaps more than once, and perhaps without telling you, and this high in-tank air pressure kept the water bladder collapsed to too-small a volume (hence causing water pump short cycling since the volume of water delivered by the pressure tank was below normal)
  
  [In our email case this seems to be what happened. The water system was feeding two houses. The naughty father-in-law in the up-hill house had overcharged the water tank air pressure with the idea that he'd see better water supply up on his hilltop.
• OR the tank water bladder was actually damaged (or plugged or not accepting water)
• OR the water bladder was partly stuck to itself giving a too-small water volume and shutting the pump off and the sticky bladder problem fixed itself when you let air out of the tank and permitted the pump to blow up the bladder to a larger, normal, un-stuck size.
• OR there was some other problem that we haven't identified, like a blocked pump control switch which was magically cured by the extra activity caused by fooling around with the system

Gas Laws and Constants, Pressures, Head Loss Equations Summary

Gas laws and constants of interest to people with home water pumps, water tanks, and maybe wells, oil storage tanks, and other pressurized liquid & gas containers such as air conditioning & heat pump systems

• 1 ATM (atmospheric pressure) = 14.7 psi at sea level
  
  if we double the pressure (Boyles Law), the psi in the tank we are using as an example would increase to about 29.4 psi.
  20 gallons of air = 2.67 cubic feet at 1 ATM.
• The D'Arcy-Weisbach equation for pressure and head loss is discussed
  
  at AIR DUCT THEORY: The D'Arcy-Weisbach formula, and
  
  at SUPPLY DUCT AIR LEAKS.
  
  This equation is used to calculate the actual pressure loss due to friction in a building piping or air duct system. (Used in its direct form below the equation may omit dominating effects of duct leaks or obstructions).
  
  Δp = λ (l / dh) (ρ v2 / 2)  
  
  Δp = pressure loss (Pa, N/m2)
  
  l = length of duct or pipe (m)
  
  dh = hydraulic diameter (m)
  
  ρ = density (kg/m3)
  
  - The Engineering Toolbox
• Boyle's Ideal Gas Law explains the relationship between gas pressure and volume:
  
  P₁V₁ = P₂V₂ all
  
  P=Pressure
  
  V=Volume
  
  at constant temperature
  
  - http://members.aol.com/profchm/boyle.html, oOr see a nice NASA animated version of Boyles Law at http://www.grc.nasa.gov/WWW/K-12/airplane/aboyle.html
  
  See BOYLE's LAW for details


• Charle's Law explains the relationship between the volume of a gas and its change with temperature.
  The volume of Gas increases with increases in temperature:
  
  V₁/T₁=V₂/T₂ 
  
  V= volume
  T= Temperature
  
  - http://members.aol.com/profchm/charles.html
  
  See CHARLES' LAW for details
• The Combined Gas Law combines the effects of Boyle's Law and Charles Law and is written as
  
  P₁V₁/T₁ = P₂V₂/T₂
  
  More about the combined gas law in a clear review is at http://members.aol.com/profchm/comb_gas.html
  
  See COMBINED GAS LAW for details


• Water Tank Laws: provides a practical explanation of pressure, temperature, volume & water tank draw-down volumes
  
  - see WATER PRESSURE TANK LAW

Using these simple gas law formulas & equations allows us to easily calculate the effect of a change in pressure, temperature, or volume of any gas in a closed container.

...

---

---

ADVERTISEMENT

---

---

Reader Q&A - also see RECOMMENDED ARTICLES & FAQs

On 2020-09-14 - by (mod) -

William

Thank you for taking time to write about Charles' Law and to suggest editing for accuracy. I will review the article accordingly and at the very least add your comments there as clarification.

Working together makes us smarter.

Daniel

On 2020-09-14 by William Slover

One of the sections that describes the temperature effect on tank pressure using Charles’ Law has a few problems. The paragraphs in question are

30gal of air (or 4 cu. ft.) of air at 33 psi and at 60 degF is changed to 90 degF (by the warming ambient air) while the container size is kept constant.

Charles would say: 4cu.ft./60degF = NEWCUFT/90degF or 0.066 = NEWCUFT/90 0.066 x 90 = NEWCUFT or about 6 cu. ft.

1. Since by the second paragraph expansion takes place, then the first paragraph’s constraint of constant container size should be removed from the first. This is consistent with the next section when it is shown that if you constrain the “container size,” pressure mustrise.

2. The expansion calculated uses degrees F. It should use absolute (degrees Rankine). Alternatively, you can use Kelvin as you did in the following section. (Incidentally unlike all other temperature scales, Kelvin is not preceded by “degrees.”

It is the SI unit for temperature and degrees is understood.)

3. Therefore, using degrees R your paragraph would be

Charles would say: 4cu.ft./520degF = NEWCUFT/550degF

or NEWCUFT = 4cu.ft./(550degF/520degF) or about 4.2 cu. ft.

Or in K

Charles would say: 4cu.ft./288K = NEWCUFT/305K
or NEWCUFT = 4cu.ft./(305K/288K) or about 4.2 cu. ft.

4. The temperature ratio is the same as used in the next section.

On 2017-05-11 - by (mod) -

Ha

Please see a detailed answer to your question at

https://inspectapedia.com/plumbing/Hot_Water_Expansion.php

Found by using our website search box to look for WATER TEMPERATURE PRESSURE INCREASE

On 2017-05-11 by ha

The effect of temperature on the water pressure inside the cylinder, pressurized water constant volume

On 2016-04-02 - by (mod) -

JM

Information about Franklin Electric SVM pressure sets is at http://franklin-electric.co.za/products/svm-pressure-sets/

This looks to me like a system that uses only a very small air charge to smooth the delivery of water to the building - avoiding rapid pump on-off switching that occurs if the tank is waterlogged.

That South African company is at

Franklin Electric South Africa (Pty) Limited
Head office and factory
PO Box 8136, Edenglen, 1613, South Africa
13 Engwena Road, Sebenza, Edenvale, 1610
Tel: +27 11 723 6500
Fax: +27 11 609 2417

Website:www.franklin-electric.com
E-mail: info@franklin-electric.co.za

The fact that you say the system "immediately loses pressure" makes me think that - as this tank does not rely on a large air pressure charge - (does it?) - either you need to re-charge the air in the tank (check the owners' manual to confirm this) OR the problem may be with the pressure sensing switch OR the pressure sensor port on the switch may be clogged: that sort of clogging is one of the most-common explanations of odd pump behaviour.

But I'm only guessing. If you can do so, give the company a call, ask for technical support, and let me know what you're told: what you learn will help other readers.

On 2016-04-02 by JM

Good Day,

I recently bought a Franklin electric SVM pressure set. Water supply comes from a tank-the pump come on and reaches a pressure of 4bar then cuts out immediately losing pressure and cutting in again. What could be possible causes of this? The tank is pressurized at 1.5bar.

Inruboerdery@gmail.com

On 2016-02-19 - by (mod) -

Thank you for the comment. You are right that the pressure and volume need review. Happily absolute and gauge will be just one ATM apart assuming sea level.

On 2016-02-19 by Anonymous

Great article, but I believe there is a math error for the Boyles law pressure tank calculation. The Boyles law equation mixed absolute and gauge pressure which would have impacted the volume determined.

Some of the FAQs discussed below are adapted from information provided by the Watts Regulator Company in a 1973 publication.[10]

Question: How much air pressure is needed in the water pressure tank?

if I have a 525 gallon tank how much air pressure do I need? - Charles Collins

Reply: the air pressure needed is not a function of water tank size but rather of the pre-charge air pressure to match the pressure control switch cut-in / cut-out pressure settings.

Re Mr. Collins question: the air pressure needed in the water tank is not a function of the tank size. If your water tank is actually 525 gallons, or if your tank is just 30 gallons, the pre-charge air pressure needed is set by the cut-in and cut-out pressures of your well pump.

Typically, when re-charging a water tank by the drainage method, if you let all of the water out of a water pressure tank you could allow air to enter tank at atmospheric pressure - which would read as "0" on your pressure gauge or would at seal level actually be about 14 psi.

If you are re-charging a water pressure tank by placing air into the tank, you set the air pressure to about 2 psi below the water tank cut-in pressure. See details about setting the water tank pressure by using the page bottom ARTICLE INDEX link

titled WATER TANK BLADDER PRESSURE ADJUSTMENT

Question: how much air volume is needed to provide 1100 gpm of water flow?

how much Air Volume for 1100 gpm water - Musyafa

Reply: air volume addresses the pressure tank draw-down cycle time

Musyafa

Running 1100 gpm is a huge flow rate, perhaps ten to twenty times a typical residential water flow rate. You'd need to multiply a common residential pressure tank size and air volume by ten; I expect you'll need a 500 to 1000 gallon pressure tank to get a reasonable draw-down cycle time.

Question: what is a pressure-heat rupture

Can you define pressure-heat rupture as it pertains to a hot water tank and can you tell me why they occur? - Anon.

Reply:

A pressure-heat rupture is a sudden bursting of a hot water tank that occurs because of the combination of high pressure and high temperature superheated water in the tank, usually along with a structural weakness in the tank itself caused often by corrosion or scale. According to the Watts Regulator Company, heat itself can have a weakening effect on a hot water storage tank.

... suppose that a water heater under 212 degF can satisfactorily withstand its service pressure of say 75 pounds (psi). However that same water heater tank, when overheated above 212 degF may only be able to withstand a pressure of 50 psi or less. So what was "normal" pressure can become "excessive pressure" when a water tank is superheated, leading to its rupture. [10]

Please see BLEVE EXPLOSIONS for details about boiling liquid vapor explosions and water heater explosions.

Question: what is thermal expansion

Reply:

See HOT WATER PRESSURE EXPANSION RATE

and THERMAL EXPANSION of MATERIALS

Question:

(Dec 22, 2011) Anonymous said:
One reason for short cycling when using a bladder tank is that the bladder has ruptured. Since there is no control on a bladder tank to admit more air it is eventually dissolved into the water ultimately resulting in little or no air remaining in the tank. Since water is incompressible the pressure reaches the cut-off pressure almost immediately and then as soon as any faucet is opened that pressure falls almost immediately to the cut-in pressure. The most obvious proof of this is water coming OUT of the air fill valve.

Reply:

Anon, thanks for the comment - we agree that a burst bladder in the water tank can lead to well pump short cycling - the water tank becomes waterlogged. Under WATER TANK BLADDERS & CAPTIVE AIR are links to articles describing diagnosing and fixing a ruptured water tank bladder.

Question:

(Feb 14, 2012) Anonymous said:
What is the calculation for how much air is to be filled in a tank for Air Pressure testing of tanks,and hydro testing of tanks

(May 27, 2012) Asjad Jamshed said:
how much litres per minute pressure tank is needed for 10 washroom, 1 kitchen, 1 laundry service room?

(Sept 24, 2014) Mohamed Essam said:
Well, if a water pump produces pressure of 10 bar to a head of 100 m, supplys a water tank on height of 100 m..how to obtain the equation gives the actual pressure on each floor coming from
01. Pipe coming from pump up to tank
02. Pipe coming from tank to ground level by gravity
thanks a lot

...

Continue reading at WATER TANK PRESSURE RELIEF VALVE or select a topic from the closely-related articles below, or see the complete ARTICLE INDEX.

Or see these

Recommended Articles

• BLEVE EXPLOSIONS - Thermal expansion in hot water tanks & piping systems, separate article
• BOYLE's LAW
• CHARLES' LAW
• COMBINED GAS LAW
• GAS LAWS & CONSTANTS
• WATER TANK BLADDER PRESSURE ADJUSTMENT where we describe adjusting air pressure in a bladder type water tank to factory specs,
• WATER TANK PRESSURE RELIEF VALVE
• WATER PRESSURE TANK LAW
• WATER TANK: USES, TROUBLESHOOTING - home
  • WATER TANK DIAGNOSIS & REPAIR
  • WATER TANK AIR, HOW TO ADD
  • WATER TANK BLADDER PRESSURE ADJUSTMENT
  • WATER TANK SIZE & VOLUME
• WATER TANK vs WATER PRESSURE

Suggested citation for this web page

WATER TANK PRESSURE CALCULATIONS at InspectApedia.com - online encyclopedia of building & environmental inspection, testing, diagnosis, repair, & problem prevention advice.

Or see this

INDEX to RELATED ARTICLES: ARTICLE INDEX to WATER SUPPLY, PUMPS TANKS WELLS & SPRINGS

Or use the SEARCH BOX found below to Ask a Question or Search InspectApedia

Ask a Question or Search InspectApedia

Try the search box just below, or if you prefer, post a question or comment in the Comments box below and we will respond promptly.

Note: appearance of your Comment below may be delayed: if your comment contains an image, photograph, web link, or text that looks to the software as if it might be a web link, your posting will appear after it has been approved by a moderator. Apologies for the delay.

Only one image can be added per comment but you can post as many comments, and therefore images, as you like.
You will not receive a notification when a response to your question has been posted.
Please bookmark this page to make it easy for you to check back for our response.
Our Comment Box is provided by Countable Web Productions countable.ca

Citations & References

In addition to any citations in the article above, a full list is available on request.

---

ADVERTISEMENT

---