 Hot Water Thermal Expansion Rate
Hot Water Thermal Expansion Rate
Hot Water Pressure Increase in Hot Water Tanks or Boilers
- POST a QUESTION or COMMENT about the expansion of water or increase of water pressure when water temperature is increased
Thermal expansion in hot water systems: This article defines thermal expansion in water equipment in response to temperature, and explains the concomitant increase in system pressure.
We show how to calculate hot water pressure increase in water heaters and boilers as a function of the increase in water temperature.
We also discuss problems that are caused by increased pressures caused by heating and thermal expansion in heating or plumbing systems.
InspectAPedia tolerates no conflicts of interest. We have no relationship with advertisers, products, or services discussed at this website.
- Daniel Friedman, Publisher/Editor/Author - See WHO ARE WE?
How to Measure or Predict the Increase of Pressure in Water Heater Tanks: Expansion Rate of Hot Water as it is Heated
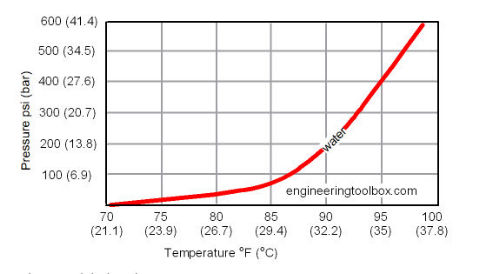 Thermal expansion in a hot water system refers to the increase in volume of water as it is heated. If the water system is closed (say by a check valve or a blockage) the result is an increase in water system pressure as well.
Thermal expansion in a hot water system refers to the increase in volume of water as it is heated. If the water system is closed (say by a check valve or a blockage) the result is an increase in water system pressure as well.
On the water temperature vs. pressure chart shown here, adapted from Engineeringtoolbox (cited below), water temperature is given on the horizontal axis.
The change in water pressure as temperature changes is given on the vertical axis.
If our water is in a closed or "water-solid" system, a change in water temperature has a corresponding change in water pressure in the system.
In a closed or "water-solid" water heating system, thermal expansion pressure equals approximately 2.5 % of volume for every 100°F rise.
Really? Well not precisely.
- For one thing the water container or tank itself will expand slightly in response to an increase in pressure.
- For another thing, a plumbing system may be restricted against backflow but not absolutely closed.
- And of course if there is an expansion tank in the system the pressure increase will be controlled so as not to cause leaking at the TPR valve.
- And finally, our friends over at engineerintoolbox.com remind us that calculating the cubic thermal or volumetric expansion of water (and some osther substances) is a bit tricky because the actual coefficient of expansion of water varies as the water temperature changes.
Hot water pressure increase in a water heater
A 40 gallon water heater with 80 PSI line pressure will build to a pressure of 145 PSI with a temperature increase of 16°F. (Brandford White 2019)
That's a 65 psi increase occurring from a 16°F temperature increase, or roughly 4 psi increase for every 1°F of temperature increase.
What makes a plumbing system closed or water-solid?
Obstructions include check valves, backflow preventers, some water meters with a built-in backflow preventer, and in some buildings, the presence of a water softener.
The actual or observed water pressure increase in a water heater as the water temperature is raised could be very little, even zero psi if the water heater is connected to open plumbing system, as the expanding water simply pushes back up the cold water lines into the cold water supply.
Watch out: But where there is an obstruction to that expansion, such as by a backflow preventer or check valve, pressure in the system will increase. The result can be a dripping temperature/pressure relief valve that can in turn become clogged, rendering the water heating system unsafe, damaging the water heater tank, or even leading to an explosion.
As the temperature increases, the maximum working pressure for which the water heater was designed (150 PSI) can be exceeded. (Brandford White 2019)
Question: How much does pressure increase inside a water heater tank (geyser) as the temperature rises?
What I need to know exactly is the following;
If you pump a geyser (water heater) full of water at ground temperature, let's say 10 degrees C, with a pump that switches off at 4 bar max, what happens to the 4 bar pressure in the geyser when you heat the water in the geyser to let's say 80 degrees C?
Or what will the maximum pressure in the geyser go up to if you start with 3 bar or 3.5 bar etc.?
In other words; if you know that the maximum possible incoming water pressure into your geyser is 4 bar, will the pressure ever increase to more than 4.5 bar which is the geyser's maximum specification? -- Bart K., South Africa.
Note: The chart of water density as a function of changes in water temperature (above left) is provided by Engineering Toolbox and is discussed in our answer, below.
Reply: Water is at its maximum density at 4 degC, and its volume (and thus pressure in a closed container) increases with temperature according to its coefficient of expansion and the degrees of temperature rise
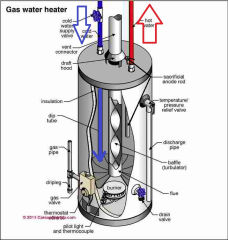 How Much Will Water Pressure Increase as Water is Heated in a Domestic Water Heater or Heating Boiler?
How Much Will Water Pressure Increase as Water is Heated in a Domestic Water Heater or Heating Boiler?
From Engineeringtoolbox cited below,
Net expansion volume of water when heated can be expressed as
Vnet = (v1 / v0 ) - 1 (1)
Vnet = expansion volume of water (ft3, m3)
V0 = specific volume of water at initial (cold) temperature (ft3/lb, m3/kg)
V1 = specific volume of water at operating (hot) temperature (ft3/lb, m3/kg)
Of course a simple and non-mathematical method of looking into the pressure that is occurring at any tank containing water and water that is heated, is discussed
at WATER PRESSURE MEASUREMENT where we simply use an instrument to measure actual water pressure that is occurring.
Hot water heater or cylinder or calorifier or geyser sketch shown here is provided courtesy of Carson Dunlop Associates, a Toronto home inspection, report writing tool & education company.
What Pressure Increase Do We Actually Observe in Water Heaters & Hot Water Heating Boilers?
Hot water pressure increase in a heating boiler: As a point of reference, in a residential hydronic heating boiler we actually observe an internal water pressure rise from 12 psi cold up to 28 psi hot as the boiler temperature increases from perhaps 60 °F up to 180 °F.
The heating boiler temperature and pressure given above are conditions much hotter than we should ever see in a domestic water heater tank where to avoid scalding hazards we limit water to about 100°F to 120°F but it is certainly possible to set water heaters to higher temperatures (and thus potentially higher pressures).
Quick Test to Detect Thermal Expansion at the Water Heater
If the TPR valve is dripping, Watts suggests this quick test:
Open a plumbing fixture during the hot water expansion period - that is, as your water is being heated up in the water heater or calorifier and while you see a drip at the temperature/pressure relief valve.
When you open a plumbing fixture such as turning on hot water at a sink or even opening a cold water faucet (assuming all of the water piping is interconnected), you immediately relieve any pressure increase in the system. If the dripping stops then you were seeing a drip caused by thermal expansion. (Watts 2011)
A second test suggested by Watts is to simply install a water pressure monitoring gauge on a hose bibb on the same building's water system. As the water heater operates you can watch the pressure increase in the system. If you use a water pressure gauge that contains a "highest pressure" indicator, such as the Watts # 276H300, you can leave the gauge on the system for 24-hours and register the highest pressure obtained.
See BLEVE EXPLOSIONS for details.
Water Heater TPR Valve Specifications
- Maximum Hot Water Temperature: With a mixing valve or tempering valve used to avoid scalding hazards installed we usually limit water heater temperature to around 120 °F. Of course it's possible to set a water heater to higher temperatures.
- TPR Valve Opening Pressure: The standard opening pressure for TPR valves on residential water heaters is usually 150 psi.
Most water heater tanks (cylinders, geysers, calorifiers) also have a standard operating pressure of 150 psi. - TPR Valve Opening Temperature: The standard maximum temperature rating for a TPR valve is usually 210°F.
Heating Boiler TPR Valve Specifications
As we discuss at GAUGES on HEATING EQUIPMENT
- Boiler TPR Valve Opening Pressure: Over 30 psi boiler pressure will cause the pressure relief valve to open.
Typical boiler pressure for a residential boiler serving a two story home would show 12 psi cold, and less than 30 psi hot. - Boiler TPR Valve Opening Temperature: At heating boiler temperatures over 200 °F we're at risk of spilling at the pressure temperature relief valve.
Typical heating boiler aquastat temperature settings on a boiler call for a Low temperature (boiler cut-in) between 120 °F and 160 °F and Typical operating temperatures on a hydronic boiler call for a high temperature (boiler cuts off) of 180-200 °F.
Calculate Water Pressure Increase in a Closed Container (water tank) due to Heating
Here we provide a more theoretical discussion of how we might calculate the pressures that can be expected to occur in a water tank due to thermal expansion.
In other words, if we start at a given or known water pressure (such as incoming building water pressure) and we then heat water in the water tank, how much will water tank pressure increase for a given rise in temperature?
The effect on water volume or density caused by changing water pressure is very small.
In general, and unlike the effects on gases when gas pressure changes, the effect of increasing pressure on the density of water (or any liquid) is very small - liquids are not very compressible.
Increasing water pressure does not have much effect on the water volume nor water density.
For example, the density of water at 3.98 °C (it's most dense temperature) is 1000 kg/m3.
The density of water at 100 °C is 958.4 kg/m3 and the density of water at 030 °C is 983.854 kg/m3. - Wikipedia and other sources.
What Are the Density and Mass of Water - What is Density?
Here we look at the effects on water pressure of increasing the water temperature. Reading about the relationship between water temperature and water pressure is confusing in part because most sources talk about water density rather than water pressure. FYI,
mass / volume = density
for any material. SI units for density are kg/m3 that is, Kilograms per cubic meter. Imperial or BG density units are in lb/ft3 or pounds per cubic foot. Technically "pounds" measures force not mass.
You can also state density in slugs/ft3 if you're arguing with an engineer. 1 slug = 32.2 pounds. Or 1 pound = 0.031 slugs.
Water has a density of 1000 kg/m3 by standard definition at its temperature of maximum density 3.98 °C and at 0% salinity.
Scientists and engineers use water as a baseline for comparing the relative density of various materials.
Water with a density of 1000 kg/m3 at 3.98 °C has a mass of 1000kg and a volume of 1 m3.
To convert the mass of 1 cubic meter of water to pressure expressed in psi and other measures:
- 1 cubic meter of water (1m H2O) = (1000 mm H2O) = 0.102 kg/cm2 = 1.42 psi
or we can convert water pressure between kg/cm2 and psi as follows: - 1000 kg/cm2 = 14,223 psi - this is the standard density of water.
Water (or anything else) exerting a pressure or force of 1000 kg/cm2 is equivalent to 14,223 psi - 1 kg/cm2 = 14.2 psi
- 1 psi = 0.0703 kg/cm2 = 0.7 m H2O = 27.7 in H2O = 2.04 in Hg
Water density vs. temperature
The density of water varies according to its temperature (see the water temperature/density charts above) but is nominally close to 1000 kg/m3, or put more accurately, at 4 °C the density of water at 1 atmosphere (sea level on earth) is 999.9720 kg/m3.
Water expands rapidly at 9% by volume when it freezes
The density of ice at 0 °C is 999.8395. So we see why ice floats, right? It's less dense than water, so takes up more volume than it did when it was a liquid, so in water an iceberg occupies more space (it has expanded from its liquid state) than the same mass of water.
How Does Water Density Change with Temperature Change?
The total change in the density of water effected by changing its temperature is small.
Density of a material changes as we vary the material's temperature or the the pressure exerted on it in a closed container - like heating up water in a water heater, calorifier, or geyser, right?
Our friends at Engineering toolbox discuss the properties of water and other fluids, and their page http://www.engineeringtoolbox.com/water-thermal-properties-d_162.html gives a chart of water and absolute pressure at various temperatures - this is the simplest answer that we trust.
Stated very simply, and assuming our water temperature starts at 4° C (it's tricky below that number as you'll read below), then
for every degree C that we increase the temperature of one unit (any unit-volume measurement) of water,
its volume (expressed in the same units) will increase by 0.000208 (cubic meters, gallons, whatever).
We are using the coefficient of thermal expansion of water = 0.00021 (1/oC)
1 deg C rise in the water tank = 0.0002 Unit Volume Rise
or if our water container is closed, such as a water heater tank, we should be able to say
1 deg C rise in the water tank = 0.0002 Unit Water Pressure Rise
Really? This may not be quite so. We are equating a unit drop in density in a closed container with an increase in pressure in the same container, but the units of measure are not necessarily identical.
Example of Water Volume Increase in a Water Heater Tank as Temperature Increases
So using your example above,
if we heat one volumetric unit (say one cubic meter, one gallon, or whatever) of water from 4 °C up to 80 °C (that's a 76 °C rise),
the new water volume (in an open container) will see an addition of 0.0152 of the original volume,
for a new total volume of 1.0152 x the original volume
Recapping:
What happens to the total volume of water in a 40-gallon water tank (geyser) when we heat it from 4 °C to 80 °C?
The volume increases from 40.0 gallons to 40.6384 gallons - doesn't sound like much, right?
Example of Water Pressure Increase in a Water Heater Tank as Temperature Increases
Let's look at water pressure change under the same temperature change.
Using the same coefficient of expansion of water as it is heated, the new total pressure (in a closed container) will be 1.052 x the original pressure [since the volume could not expand the pressure must increase instead].
If our starting water pressure in the water tank was 4 bar then we think this same calculator (or equation) work as well and our new water pressure in the closed tank is 4.0638 bar.
Stating the same amounts in PSI for North Americans, our water tank pressure is increasing from 4 bar = 58 psi, up to 67.2 psi, or about 10 psi of increase in pressure - if we've got this right.
(1 bar = 14.5 psi, so that's about 58 psi, or 1 psi = 0.06895 bar)
Reader Anthony Lee comments:
When converting the “new” pressure of 4.0638 bar to psi you have multiplied by 4.638 instead of 4.0638. The new pressure if 58.9 psi and not 67.2 psi
[That gives us one tenth as much pressure increase or just 1 psi per degree C not ten psi - Ed.]
Watch out for hot water scalding hazards and unsafe water tank or calorifier pressures: By the way, typical safe temperatures in water heaters or calorifiers used for washing and bathing are around 104 degF up to a max (and risk of scalding) of 120 degF, or from at about 40-49 °C so our reader's example of superheating geyser water to 80 °C is scary.
See WATER HEATER SAFETY for details.
Making a new example for domestic water heating, entering water temperature in North America is around 10 °C or 50 °F (or colder, below 40°F in northern areas such as northern Minnesota).
If we heat 40 gallons of water (a typical domestic water heater or calorifier size) from 40 °F (a cold state) up to 120 °F (hotter than most manufacturers recommend and about the limit you'd expect), then our new water tank volume would be 40.672 gallons [IF the tank were an open vessel].
Typically the pressure/temperature relief valves on domestic water heaters are set to open at 100, 125, or 150 psi (6.9, 8.61, or 10.34 bar).
Worst Case Water Heater Pressure Analysis
What happens if we start with 20 psi water in our water heater (calorifier or geyser) tank that has entered from our well at 40 °F, and we do two things:
we turn on our water heater to heat the tank contents up to 120 °F,
and our pump has turned on to pump up starting pressure in the water heater tank to 50 psi. We have
- Water pressure increases from 20 to 50 psi or + 30 psi
- Water temperature increases from 40 °F to 120 °F or + 80 °F
Engineering Toolbox guys and gals inform us that the formula to calculate the effect on density of changing both water pressure and water temperature at the same time is calculated as
ρ1 = [ ρ0 / (1 + β (t1 - t0)) ] / [1 - (p1 - p0) / E]
Plugging in what we know:
ρ1 = [ 999.97ρ0 / (1 + 0.0002β (t1 - 4.44t0)) ] / [1 - (p1 - 999.97p0) / 2.15 109E]
where [ this needs a scientific calculator or software]- Ed.
- ρ1 = final density (kg/m3)
- ρ0 = 999.97 = initial density (kg/m3) water at 40 oF or 4.444 oC
- β = 0.0002 = volumetric temperature expansion coefficient (m3/m3 oC)
- t1 = final temperature (oC)
- t0 = 4.44 = initial temperature (oC) (40 degF = 4.4444 oC)
- E = 2.15 109 = bulk modulus fluid elasticity - E - of water
Watch out: this is not actually the very worst case of a possible hot water pressure increase to dangerous levels in a building.
For example at a property served by a municipal water main, incoming water pressures can be higher than those produced by a private well pump if someone has tampered with a pressure regulating valve.
The equation behind this calculation and a nice online water density calculator are discussed at ET's Online Water Expansion Calculator
BLEVE EXPLOSIONS or boiling liquid vapor expansion explosions can occur at both domestic water heaters (calorifiers or geysers) and at hot water heating boilers (hydronic heating systems).
We discuss the role of pressure/temperature relief valves in protecting against these hazards
at RELIEF VALVE, TP VALVE, BOILEr
and at RELIEF VALVE, WATER HEATER
At THERMAL EXPANSION TPR VALVE LEAKS we explain how normal thermal expansion in a hot water system can cause pressure & temperature relief valve leaks that in turn can lead to valve failure and a dangerous risk of a BLEVE.
At MEASURE WATER SYSTEM PRESSURE & PRESSURE MAXIMUM we explain how to make or buy an inexpensive recording-type water pressure test gauge to detect thermal expansion T&P valve leaks.
At HOT WATER EXPANSION TANKS we explain the use of expansion tanks or relief valves designed specifically to handle thermal-expansion leaks in hot water systems.
More Detailed Explanation of the Pressure, Density, and Volume Behavior of Water as Water is Heated in a Closed Container
Our second recommended source is in academia at UCSC - Physics dept. See http://physics.ucsc.edu/~keivan/THERMO5D/sol1.pdf that gives the non-linear coefficient of volume expansion for water vs. temperature.
And we presume you know that water actually expands when it freezes, but because of the crystalline structure it forms. Water can expand in two temperature directions (if we include freezing) - confusing the discussion.
It's interesting how answers to the question: "how much does water expand when heated" vary on the web all over the place. Examples of some statements we found [web search 09/16/2010]
When water is heated it expands rapidly adding about 9 % by volume. - this is probably not quite correct as the expansion rate for heated water is not linear. So when we heat water from freezing, it actually contracts in volume, up to its maximum density point. Water has its maximum density at 3.98 degrees C.
From 3.5 degrees to 4.5 degrees water doesn't expand at all. - this answer doesn't quite agree with the one above
Water between 0 and 4 degrees Celsius will contract when heated - this is consistent with the explanation about expanding when freezing but we think some of the writers are sloppy with the decimal point and precision.
Also see the wikipedia entry http://en.wikipedia.org/wiki/Properties_of_water - and Wiki on thermal expansion at http://en.wikipedia.org/wiki/Thermal_expansion
What are the Thermal Coefficients of Expansion for Water?
The thermal coefficient of expansion of water is 0.00021 per 1 °C at 20 °C
The thermal expansion coefficients for water varying by temperature are at http://physics.info/expansion/
How do Fluids Behave When Heated - Fluid Density, Coefficient of Expansion, Temperature Rise
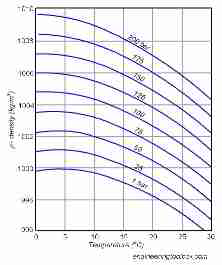
A nice web page about density of fluids and a chart plotting the density of water at different temperatures is at The Engineering Toolbox, from which we quote below [with permission].
If you consider that a decrease in the density of a fluid in a closed container is analogous to a concomitant increase in the fluid pressure in that container, we're almost home-free on the question of the amount of expansion in water as it is heated.
Notice in the curves on this chart (click to enlarge) of water density (or water pressure) that as our little quotes above illustrated, the density of water increases (pressure decreases) as water temperature increases from 0 to around 4 C, then above that temperature the density of water decreases (water pressure increases) as the water temperature rises.
But since the water pressure vs. water temperature lines are not straight (they're curved) while you can read the approximate density (or pressure) change as a function of water temperature right off the chart shown here, to know the precise change in water pressure if it is heated from one temperature to another requires some calculation.
In this chart, the left side or vertical axis is water density, measured in kilograms / cubic meter or kg/m3 , and the horizontal axis is water temperature measured in oC.
Conversely if we hold density constant and heat water, the pressure would increase on the same scale as shown here.
Density Change in Water When Water Temperature is Changed
The density of a fluid can be expressed as
ρ1 = ρ0 / (1 + β (t1 - t0))
[This is Engineering Toolbox equation # (1)]
where
- ρ1 = final density (kg/m3)
- ρ0 = initial density (kg/m3)
- β = volumetric temperature expansion coefficient (m3/m3 oC)
- t1 = final temperature (oC)
- t0 = initial temperature (oC)
The Volumetric Temperature Coefficient - β for water = 0.0002 (m3/m3 oC)
Water density and change in water pressure
When water pressure [or the pressure of a fluid] is changed, the density of a fluid can be expressed as
ρ1 = ρ0 / (1 - (p1 - p0) / E)
[This is Engineering Toolbox equation # (2)]
where
- E = bulk modulus fluid elasticity (N/m2)
- ρ1 = final density (kg/m3)
- ρ0 = initial density (kg/m3)
- p1 = final pressure (N/m2)
- p0 = initial pressure (N/m2)
The bulk modulus fluid elasticity - E - of water = 2.15 109 (N/m2)
What Happens When We Simultaneously Change Both Water Pressure and Water Temperature in a Water Heater Tank?
For example, the static water pressure in a water heater (or geyser) tank at a fixed temperature might be X psi. But two different events affect the pressure and density of water in the tank:
- The water supply source pressure varies, for example from a private well and pump system, will deliver water at varying pressures.
So the psi in a water tank may sit at 20 just before the water pump comes on, and may rise to 40 psi or even 50 psi just as the water pump cuts off. - The water temperature varies: temperatures inside the water heater will vary as the water heating source (an electric element, gas burner, oil burner, solar source, other) is turned on and off by a thermostat.
So you can see that there are two forces, both temperature and pressure, at work at once. One way to translate these into a single number is to look at the change in water density.
Our friends at Engineering Toolbox provide this general equation relating the density of a fluid to changes in both temperature and pressure, combining the information given above in equations #(1) and #(2):
ρ1 = [ ρ0 / (1 + β (t1 - t0)) ] / [1 - (p1 - p0) / E]
ET's Online Water Expansion Calculator
The Engineering Toolbox also gives us a nice online calculator of the volumetric (or cubic) expansion of a substance as a function of starting volume, density, and mass.
The volumetric temperature coefficient of water is given as water : 0.00021 (1/oC) in other words, this is water's coefficient of volumetric expansion as it is heated.
Their calculator is at http://www.engineeringtoolbox.com/volumetric-temperature-expansion-d_315.html
The equation to calculate the change in units volume of water when the water temperature changes is given by ET as
dV = V0 β (t1 - t0)
- dV = V1 - V0 = change in volume (m3)
- β = volumetric temperature expansion coefficient (m3/m3 oC)
- t1 = final temperature (oC)
- t0 = initial temperature (oC)
Similarly, the equation to calculate the change in units density of water when the water temperature is changed is given by ET as
ρ1 = m / V0 (1 + β (t1 - t0))
= ρ0 / (1 + β (t1 - t0))
- ρ1 = final density (kg/m3)
- ρ0 = initial density (kg/m3)
Last, and least necessary for our water pressure change above, ET provides the formula for the specific volume of a unit as a function of its density and mass
Specific volume of a unit can be expressed as
v = 1 / ρ = V / m
- v = specific volume (m3/kg)
- ρ = density (kg/m3)
- V = volume of unit (m3)
- m = mass of unit (kg)
Some Properties and Constants of Water Used in Calculations of Pressure, Temperature, Volume, and Density of Water
- The bulk modulus fluid elasticity - E - of water = 2.15 109 (N/m2)
- The thermal coefficient of expansion of water is 0.00021 per 1 °C at 20 °C
- Density of water: [we mean fresh water, not seawater] expressed in kg/m3
Water Temperature °C |
Water Density kg/m3 |
Pressure psi lb/in2 |
Pressure kg/m2 |
Pounds per cubic inch |
Water Mass kg |
Water Volume Unit Volume |
|---|---|---|---|---|---|---|
| 100 | 958.4 | 0.0346244 | ||||
| 80 | 971.8 | 0.0351085 | ||||
| 60 | 983.2 | 0.0355204 | ||||
| 30 | 995.6502 | 0.0359701 | ||||
| 15 | 999.1026 | 0.0360949 | ||||
| 3.98 | 1000 | 14,223 psi (1) | 0.0361263 | 1000 | 1 [e.g. 1m3] | |
| 0 | 999.8395 | 0.0361215 |
- Water is at its highest density at 3.98 °C = 1000 kg/m3 or 1 g/cm3. The correct SI unit of density of water is
ρ = 1000 kg/m3. [also FYI, 1 m3 = 1,000,000 cm3] - Specific weight of water = 62.4 lb/ft3 (IU) or 9.81 kN/m3
- Specific weight of seawater = 64 lb/ft3 (IU) or 10.1 kN/m3 - must be all that extra salt making it more dense, so we float better in seawater than in fresh water, right?
- Specific gravity of water: At its maximum density of 4 °C (39 °F) the specific gravity of water is 1.
Notes:
Conversions of density, mass, pounds, slugs, and psi (pounds per square inch)
A mass of 1000kg pressing on an area of 1 m2, that is on the bottom of the one meter square cube, means that the pressure on the cube bottom is also 1000 kg over 1 m2.
- 1000 kg/cm2 = 14,223 psi
- 1000 kg/m2 = 142,231 psi
- 1 atmosphere = 14.69 psi
- 1 mm H2O = 0.00145 psi
- 1 mm Hg = 0.49 psi
- 1 inch H2O = 0.036 psi
- 1 kg/cm2 = 14.21 psi
- 1 m H2O = 1.45 psi
- 1 mm H2O = 0.00045 psi or 1.45 10-3
- 1000 kg = 68.5 slug
- 2020/08/19 Lasse said: Conversion above list 1000 kg/m2 = 142,231 psi.
That's wrong.
0.1 kg/cm2 = 1,000 kg/m2 = 1.422 psi (whereas "," thousands separator and "." is decimal symbol)
1000kg/cm2 = 10,000,000 kg/m2 = 14,223 psi
How to convert density to pressure
The density of any object or material is its mass per unit of volume.
The pressure exerted by an object or material is its force per unit of area.
If we know the density and the volume of any area we can thus calculate the pressure that it can exert per unit of area.
1. Calculate the mass of a material: volume x density = mass.
2. Calculate the pressure or force: mass / area = pressure per unit of area.
See WATER PRESSURE MEASUREMENT for a detailed example of calculating the water pressure at the bottom of a well. There you'll see that The pressure of a column of water is about 0.433 psi per foot of water column height.
Why any object floats or sinks: If the total volume of water displaced by any object (if that object could be pushed totally under water) has more mass than the object itself has, then that object will float with at least some part of its shape above the top level of water.
If an object has mass exactly the same as the mass of water displaced by its volume, it is neutrally buoyant (at the surface of the water) and floats with its top just touching the top surface of the water. We like to think of this as the surrounding water and its mass "pushing" on the object on all sides, pushing it "up" into the air (or atmosphere at sea level).
If an object weighs more than the water displaced by its total volume (or speaking correctly if it has more mass), it sinks.
Hot Water Pressure & Expansion by Temperature: Research
- Also seeReferences or Citations at the end of this document
- Bradford White, PRESSURE DAMAGED WATER HEATERS (#115) [PDF] (2019) retrieved 2020/01/11 original source: https://www.bradfordwhite.com/pressure-damaged-water-heaters-115/#
- CIBSE, HYRDONIC SYSTEM DESIGN, Appendix 1.A1 [PDF] CIBSE,
222 Balham High Road
London
SW12 9BS
United Kingdom
Tel +44 (0)20 8675 5211
Fax +44 (0)20 8675 5449 Email: membership@cibse.org
This document discusses the importance of designing hydronic systems to include handling the increase in pressure that occurs when water is heated. Retrieved 2018/09/30, oiginal source: www.cibse.org/getmedia/76229a96-c37e-4d2f-b4f9-7d62ba62bab4/Guide-B1-appendix.pdf.aspx
CIBSE is a UK association, the Chartered Institute of Building Services Engineers, https://www.cibse.org/
- Cleaver Brooks, HOT WATER SYSTEMS [PDF], Cleaver-Brooks
221 Law Street
Thomasville, GA 31792 USA, Tel: 229-226-3024
800-250-5883 Email:
info@cleaverbrooks.com Retrieved 2018/09/30, original source: http://cleaverbrooks.com/reference-center/boiler-basics/Hot Water Systems.pdf
Website Excerpt:
Cleaver-Brooks is a complete boiler room solutions provider that helps businesses run better every day.
It develops hot water and steam generation products aimed at integrating and optimizing the total boiler/burner/control/stack exhaust system to maximize energy efficiency and reliability while minimizing emissions. - Engineering Toolbox, Density of Liquids versus Change in Pressure and Temperature, retrieved 2020/01/11 original source: https://www.engineeringtoolbox.com/fluid-density-temperature-pressure-d_309.html
- Engineering Toolbox, Sizing Hot Water Expansion Tanks, retrieved 2020/01/11 original source: https://www.engineeringtoolbox.com/expansion-tanks-d_885.html
- Guyer, J. Paul, P.E., R.A., INTRODUCTION TO HIGH TEMPERATURE
WATER HEATING PLANTS [PDF] (2011), Guyer Partners,
44240 Clubhouse Drive
El Macero, CA 95618 USA Tel:
(530) 758-6637 Email:
jpguyer@pacbell.net posted by CED Engineering, Continuing Education and Development, Inc.
9 Greyridge Farm Court
Stony Point, NY 10980 USA, Tel: (877) 322-5800, Email: info@cedengineering.com , retrieved 29018/09/30, original source: https://www.cedengineering.com/userfiles/Intro%20to%20HTW%20Heating%20Plants.pdf
Note: This course is adapted from the Unified Facilities Criteria of the United States government, which is in the public domain, has unlimited distribution and is not copyrighted. - Stack Exchange, Physics, "Water pressure vs temperature", retrieved 2020/01/11 original source: https://physics.stackexchange.com/questions/363328/water-pressure-vs-temperature
- U.S. Department of Defense, UNIFIED FACILITIES CRITERIA (UFC) [PDF], UFC 1-300-09N 25 May 2005 Including Change 9, 1 July 2013 retrieved 2018/09/30, original source: https://www.navfac.navy.mil/content/dam/navfac/NAVFAC Atlantic/NAVFAC Mid-Atlantic/PDFs/PWD_Maine_Capital_Improvements/ufc_1_300_09n.pdf
- [9] Watts, 815 Chestnut Street, North Andover, MA, USA 01845-6098, Website: http://www.watts.com web search 09/18/2010 original source: http://www.watts.com/pages/learnAbout/reducingValves.asp?catId=64
- Watts, SPECIFICATIONS AND SELECTION FOR TEMPERATURE AND PRESSURE PROTECTION OF WATER HEATERS AND HOT WATER STORAGE TANKS [PDF] (1996) Op. Cit., retrieved 2020/01/11 original source: http://media.wattswater.com/F-SF.pdf
- [10] 52 Questions and their Answers [about] Hot Water [Heaters, Explosions & Water Heater Safety], Watts Regulator Company (1973) retrived anew 2018/10/27, original source: http://media.wattswater.com/f-52qa.pdf
...
Reader Comments, Questions & Answers About The Article Above
Below you will find questions and answers previously posted on this page at its page bottom reader comment box.
Reader Q&A - also see RECOMMENDED ARTICLES & FAQs
On 2020-05-27 - by (mod) - T/P relief valve on my hot water heater is weeping about 1 cup of water every time it heats
Mike
Let's start by taking a look (well you for now) at the diagnostics at
RELIEF VALVE LEAKS
where we list various causes of T/P relief valve leaks.
When you're confident the problem isn't the valve itself you look at the starting water pressure, the temperatures involved, and external causes like water hammer or hot water expansion.
That
last is discussed at HOT WATER PRESSURE EXPANSION RATE - how much does water expand when you heat it?
In that article you'll find our excerpt from a water heater manufacturer (Bradford White) that notes that
A 40 gallon water heater with 80 PSI line pressure will build to a pressure of 145 PSI with a temperature increase of 16°F. (Brandford White 2019)
So it's entirely possible that your water heater's size and starting water inlet temperature and pressure are sufficient that when you heat the water up to 120 degF the internal pressure in the heater exceeds 150 psi and the TPR valve is opening just as it was intended to do.
Then see HOT WATER EXPANSION TANKS - cure the problem of leaks in heated hot water systems, calorifiers, water cylinders
On 2020-05-27 by Mike
The T/P relief valve on my hot water heater is weeping about 1 cup of water every time it heats. The incoming water pressure is gauge checked at 60 psi and the temperature is 120 degrees checked with a thermometer.
The valve is calibrated at 150 psi and the temperature at 210 degrees.
What's going on?
No, it's not the T/P relief valve.
I've replaced it with 2 NEW ones and the problem persists. I've been here for 33 years and this has never happened.
This Q&A were posted originally
at RELIEF VALVE, WATER HEATER DIAGNOSTIC FAQs-2
On 2018-09-30 - by (mod) -
Thank you for the query, Jim. I'm not familiar with the tables you cite, nor the fractions you cite. 1/23 sounds like way too much volume increase for a single degree of temperature rise.
If you have a reference citation I'd be glad to add that information and meanwhile will look further myself.
For other readers,
CIBSE is a UK association, the Chartered Institute of Building Services Engineers, https://www.cibse.org/
CIBSE
222 Balham High Road
London
SW12 9BS
United Kingdom
Tel +44 (0)20 8675 5211
Fax +44 (0)20 8675 5449
For membership enquiries: membership@cibse.org
This CIBSE document
Appendix 1.A1 Hydronic system design, [PDF]
discusses the importance of designing hydronic systems to include handling the increase in pressure that occurs when water is heated.
Original source: http://www.cibse.org/getmedia/76229a96-c37e-4d2f-b4f9-7d62ba62bab4/Guide-B1-appendix.pdf.aspx as retrieved 2018/09/30
On 2018-09-30 by Jim
What happened to the simple increase in volume of 1/23 (1/25) for 0-100 temperature difference. CIBSE tables?
On 2017-03-17 - by (mod) -
Lerato
Be sure to also see THERMAL EXPANSION of MATERIALS where we give the coefficients of thermal expansion for many building materials.
and an interesting application of this approach is at SIDING, FIBER CEMENT GAPS
On 2017-03-17 - by (mod) - convert a coefficient of thermal expansion of a material to an expansion rate
Lerato
The coefficient of expansion gives us the increase in dimension as a change between two temperature points.
An expansion "rate" would, if I am guessing at what you're actually asking, express expansion of a material's dimension over time in response to temperature change.
My suggestion would be to plot the temperature change itself over that time = that is temperature of the material not just ambient temperature as there will be a delay or lag due to thermal mass and the effect of the material being in contact with other materials, sheltered from temperature, wind, sun, etc. (So you see it's complex if you want to do it right)
Once you have the temperature change of your material over time you can simply calculate, based on the coefficient of expansion, just how much the material has changed in dimension over time by correlating it to the temperature change over the same time interval. It's a simple plot.
On 2017-03-17 by LERATO
How do I convert a coefficient of thermal expansion of a material to an expansion rate?
...
Continue reading at BLEVE EXPLOSIONS - why water heater tanks or calorifiers might explode if the relief valve fails, or select a topic from the closely-related articles below, or see the complete ARTICLE INDEX.
Or see HOT WATER PRESSURE EXPANSION FAQs questions & answers posted originally at this article
Or see these
Recommended Articles
- BLEVE EXPLOSIONS
- EXPANSIVE FORCE of FREEZING WATER
- HOT WATER PRESSURE EXPANSION RATE
- HOT WATER EXPANSION TANKS - cure the problem of leaks in heated hot water systems, calorifiers, water cylinders
- RELIEF VALVE, WATER HEATER - home
- RELIEF VALVE LEAKS diagnose leaks at TPR valves
- THERMAL EXPANSION of MATERIALS
- THERMAL EXPANSION TPR VALVE LEAKS - why the relief valve leaks when heating water
Suggested citation for this web page
HOT WATER PRESSURE EXPANSION RATE at InspectApedia.com - online encyclopedia of building & environmental inspection, testing, diagnosis, repair, & problem prevention advice.
Or see this
INDEX to RELATED ARTICLES: ARTICLE INDEX to T&P RELIEF VALVES
Or use the SEARCH BOX found below to Ask a Question or Search InspectApedia
Or see
INDEX to RELATED ARTICLES: ARTICLE INDEX to PLUMBING SYSTEMS
Or use the SEARCH BOX found below to Ask a Question or Search InspectApedia
Ask a Question or Search InspectApedia
Try the search box just below, or if you prefer, post a question or comment in the Comments box below and we will respond promptly.
Search the InspectApedia website
Note: appearance of your Comment below may be delayed: if your comment contains an image, photograph, web link, or text that looks to the software as if it might be a web link, your posting will appear after it has been approved by a moderator. Apologies for the delay.
Only one image can be added per comment but you can post as many comments, and therefore images, as you like.
You will not receive a notification when a response to your question has been posted.
Please bookmark this page to make it easy for you to check back for our response.
IF above you see "Comment Form is loading comments..." then COMMENT BOX - countable.ca / bawkbox.com IS NOT WORKING.
In any case you are welcome to send an email directly to us at InspectApedia.com at editor@inspectApedia.com
We'll reply to you directly. Please help us help you by noting, in your email, the URL of the InspectApedia page where you wanted to comment.
Citations & References
In addition to any citations in the article above, a full list is available on request.
- Thanks to careful reader Anthony Lee in the U.K. for editing and accuracy comments, June 2012.
- Watts, 815 Chestnut Street, North Andover, MA, USA 01845-6098, web search 09/18/2010 Watts Regulator Corporation, 815 Chestnut Street, North Andover, MA, USA 01845-6098, provides pressure and temperature relief valves, water pressure test gauges, water pressure regulators, backflow preventers, check valves, and other plumbing and heating controls and supplies. Website: http://www.watts.com/
- Watts Backflow preventers - 978-688-1811
- Watts Control valves - 713-943-0688 for example Watts pressure reducing valves, original source: http://www.watts.com/pages/learnAbout/reducingValves.asp?catId=64
- Watts Drainage products - 828-288-2179
- Watts Potable water PEX plumbing - 978-688-1811
- Watts Water safety controls - 978-688-1811
- Watts Water quality & conditioning products - 352-465-2000
- Engineering toolbox properties of water - http://www.engineeringtoolbox.com/water-thermal-properties-d_162.html editor.engineeringtoolbox@gmail.com web search 09/16/2010
- SI Metric.co.uk provides tables and constants for the properties of water - web search 09/16/2010 original source: http://www.simetric.co.uk/si_water.htm
- Wikipedia on the Density of water at 1 atmosphere, web search 09/16/2010, original source: http://en.wikipedia.org/wiki/Density
- In addition to citations & references found in this article, see the research citations given at the end of the related articles found at our suggested
CONTINUE READING or RECOMMENDED ARTICLES.
- Carson, Dunlop & Associates Ltd., 120 Carlton Street Suite 407, Toronto ON M5A 4K2. Tel: (416) 964-9415 1-800-268-7070 Email: info@carsondunlop.com. Alan Carson is a past president of ASHI, the American Society of Home Inspectors.
Thanks to Alan Carson and Bob Dunlop, for permission for InspectAPedia to use text excerpts from The HOME REFERENCE BOOK - the Encyclopedia of Homes and to use illustrations from The ILLUSTRATED HOME .
Carson Dunlop Associates provides extensive home inspection education and report writing material. In gratitude we provide links to tsome Carson Dunlop Associates products and services.

