The Combined Gas Law: this article describes and defines the Combined Gas Law with examples of using the Combined Gas Law to join the effects of pressure, temperature, and initial volume to explain what happens to air in a water storage tank, LP gas in a gas tank, oil & fumes in an oil storage tank, or air conditioning /heat pump refrigerant liquid & gas volumes inside of an air conditioning or heat pump system.

Definition & Practical Applications of the Combined Gas Law

The Combined Gas Law combines the effects of Boyle's Law and Charles Law thus considering gas pressure, gas volume, and gas temperature all together. The Combined Gas Law is written as

P₁V₁/T₁ = P₂V₂/T₂

where

P = Pressure of the gas

V = Volume occupied by the gas

T = Temperature of the gas

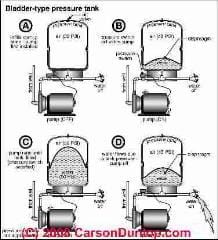
Example of using the Combined Gas Law to Explain What Happens Inside of a Water Pressure Tank

But inside of our water tank the total space available for air is fixed by the physical size of the tank itself. If we're talking about air inside a water tank, the volume taken up by the air can't get bigger than the tank itself.

Charles and Boyle considered individually don't tell us what happens to the air pressure and volume inside of a water tank as temperatures change.

To figure this out we need to look at pressure and temperature simultaneously using the

Combined Gas Law:   P₁V₁/T₁ = P₂V₂/T₂ 

along with some simple algebra. I'm slow at math so we have to show every step in the calculation before I'll believe it.

• Starting Formula: (33 psi X 4 cu. ft.) / 60degF = (NEWPSI X 4 cu. ft.) / 90degF
• Before using these temperatures with the gas laws they must be converted to Kelvins. The formulas for these conversions between Kelvin and Fahrenheit or Centigrade are given just above where we introduced Charle's Law. (Note 1 below).
  Convert our starting temperature 60 degF to Kelvins: K₁ = (60 degF + 460)/1.8 = 288 degK
  Convert our ending temperature 90 degF to Kelvins: K₂ = (90 degF + 460)/1.8 = 305 degK
• Corrected Combined Gas Law Formula: (33 psi X 4 cu. ft.) / 288 degK = (NEWPSI x 4 cu. ft.) / 305 degK
• 132 / 288 = (NEWPSI x 4) / 305
• .46 = (NEWPSI x 4) / 305
• .46 x 305 = NEWPSI x 4
• 140 = NEWPSI x 4
• 140/4 = NEWPSI
• 35 = NEWPSI - so we went from 33 psi to 35 psi when we increased the temperature of the air in the tank from 60 degF. to 90 degF.
• (35-33)/33 = .06 or in other words, we see about a 6% increase in pressure in the water tank when the temperature changes from 60 degF. to 90 deg.F.

One would conclude from this calculation that the effects of normal temperature changes in the environment of a water pressure tank will not have a significant effect on the in-tank pressure.

Note 1: A thoughtful reader pointed out that the measurement of temperature in these basic formulas must be counted from absolute zero, (-273 degrees Centigrade / -460 degrees Fahrenheit). Our references for Charle's Law confirm this requirement. Another simpler calculation of the effects of temperature change on water pressure tank internal pressures was suggested by Mr. Pryor.

The difference between the starting and ending temperatures in degF. is divided by the starting temperature converted to Kelvins: a temperature change from 60 degF to 90 degF is (90-60)/(460+60) = 5.77% which is indeed only a small increase in pressure inside the water tank.

...

Continue reading at at WATER PRESSURE TANK LAW or select a topic from closely-related articles below, or see our complete INDEX to RELATED ARTICLES. or select a topic from the closely-related articles below, or see the complete ARTICLE INDEX.

Or see these

Recommended Articles

• GAS LAWS & CONSTANTS
  • BOYLE's LAW
  • CHARLES' LAW
  • COMBINED GAS LAW
  • REFRIGERANT PRESSURE READINGS & CHARTS
  • WATER PRESSURE TANK LAW
• OIL TANK PRESSURE
• OPERATING TEMPERATURES HVAC
• PRESSURE CONTROLS & SAFETY SWITCHES
• REFRIGERANT GASES & PIPING
• WATER TANK AIR PRESSURE ADJUSTMENT
• WATER TANK PRESSURE CALCULATIONS

Suggested citation for this web page

COMBINED GAS LAW at InspectApedia.com - online encyclopedia of building & environmental inspection, testing, diagnosis, repair, & problem prevention advice.

Or see this

INDEX to RELATED ARTICLES: ARTICLE INDEX to AIR CONDITIONING & HEAT PUMPS

Or use the SEARCH BOX found below to Ask a Question or Search InspectApedia

Ask a Question or Search InspectApedia

Try the search box just below, or if you prefer, post a question or comment in the Comments box below and we will respond promptly.

Note: appearance of your Comment below may be delayed: if your comment contains an image, photograph, web link, or text that looks to the software as if it might be a web link, your posting will appear after it has been approved by a moderator. Apologies for the delay.

Only one image can be added per comment but you can post as many comments, and therefore images, as you like.
You will not receive a notification when a response to your question has been posted.
Please bookmark this page to make it easy for you to check back for our response.
Our Comment Box is provided by Countable Web Productions countable.ca

Citations & References

In addition to any citations in the article above, a full list is available on request.

---

ADVERTISEMENT

---