Definition of well water static head height, total dynamic head and other definitions in well construction:

Here we define the static head in a well and we explain how the well's static head can compensate for a well with a poor flow rate.

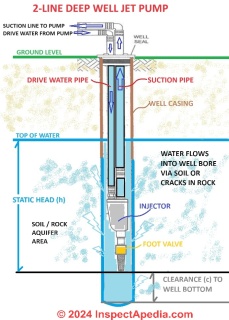
Our page top drawing illustrates the initial head or static head in a well using a 2-line deep well jet pump. 

The static head is basically a reservoir of water in the well bore or casing. It might be significant or trivial, but depending on your well bore recovery rate, the size of the static head can make the difference between a usable well with a low flow rate and running out of water. Also if you don't understand well static head you can be fooled by a "well flow test" result.

Static Head Height: Well Water Starting Quantity - What is the Static Head of Water in the Well?

This article gives the definitions for common well construction and diagnosis terms that are needed to assess well flow rate, volume, and pressure.

The actual steps on how to calculate the water volume in your well can now be found

at WELL WATER VOLUME CALCULATION

series describes how we measure the amount of water available and the water delivery rate ability of various types of drinking water sources like wells, cisterns, dug wells, drilled wells, artesian wells and well and water pump equipment.

How is well quantity measured? How do well static head volume, height, pressure vary over time?

Question: What happens to well flow when we install a more powerful water pump? Answer: We exhaust the well static head volume more quickly.

[Click to enlarge any image]

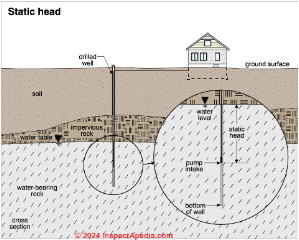
This sketch, courtesy of Carson Dunlop Associates offers a graphic explanation of well static head. The static head in a well is is not the total amount of water than can be pumped out of the well, it's just where we start.

 

Article Contents

• DEFINITIONS - WATER WELL HYDRAULICS
• STATIC HEAD VOLUME
• STATIC HEAD PRESSURE = PRESSURE HEAD
• STATIC HEIGHT = DISCHARGE HEAD
• HYDROSTATIC PRESSURE / BOTTOM HOLE PRESSURE
• TOTAL DYNAMIC HEAD
• STATIC LIFT = SUCTION HEAD
• HEAD LOSS = FRICTION LOSS
• WHY STATIC HEAD HEIGHT VOLUME CHANGES

Definitions of Static Head, Static Height, Static Lift, Total Dynamic Head (TDH) in a Well

Definition of Well Water Static Head Height or Static Well Volume

The static head volume (as used here) is the actual volume of water that is inside a well bore, cylinder or dug well when the well is at rest (not in use) and after it has fully recovered from prior or recent use.

The static head volume inside a water well tells us how much water is available to the pump after the well has rested, water has risen to its maximum height inside the well, and the pump is about to turn on.

As we will explain below, because (except in some flowing artesian wells) water does not rise all the way to the top of the well bore or dug well opening, the static head volume is less than the total volume of the interior of the well bore.

Definition of Static Pressure Head or Pressure Head

Static pressure head - the water pressure measured at the bottom of a column of water when the well is at rest and fully recovered. Static pressure head in this use could for clarity be called pressure head, or static head pressure.

The word "static" is important here. The pressure head at the bottom of the column of water in a well is strictly a function of the height of the water column (the diameter is irrelevant as you'll read in calculations later in this article).

When a water well is at rest and has fully recovered, the static head height, static head volume, and static head pressure or pressure head are all at their maximum.

Once a well pump begins running and the level of water inside the well bore is drawn down, the height of the water column in the well as well as pressure head will be reduced.

As the pump continues to run, the pressure head is not static but rather is dynamic, changing as the water level continues to drop.

What's the water pressure at the bottom of a well, as exerted by the column of water in the well?

Static head pressure: The PSI of water pressure at the base of a column of water of height H in feet = H x 0.433 psi

Pressure at the water well bottom increases by 0.433 psi per foot of height of water.

Example: If your well has a static head height of 100 feet, the water pressure at the bottom of that static head = static head pressure would be 100 x 0.433 = 43.3 psi.

Here's the math, simplified:

One 12x12" cube of water that is 12" high (one cubic foot) with a weight of 62.4 pounds (per cubic foot) exerts 62.4 psi over an area of (12x12) 144 square inches.

The psi (pounds per square inch) of force exerted by that cubic foot (a 12" high square of water) = 62.4 pounds / 144 sq.in. = 0.433 psi.

Only the height of the water column matters, not its diameter nor its shape. (And of course the force of gravity).

So a 1" tall column of water of any shape (including a round well bore) also exerts 0.433 psi as measured at the bottom of the column.

Details are at DEFINE WATER PRESSURE per FOOT of HEIGHT where we consider the weight of water. When at rest, the vertical pressure gradient in a column of water such as in a well bore depends only on the weight of the water.

Definition of Static Height or Discharge Head

A related but not identical well construction term of importance is

Static height, also referred to as discharge head: the maximum height that a pump has to lift water from the point of pickup.

Static height is typically higher than the static head (as used above) because the well water pipe in the well bore rises well above the top of the static water column to reach its exit point either at the casing top or at a pitless adapter from which piping continues onwards to the water destination.

If the well piping has to run uphill from the well exit to the building or to the water tank destination, that added height must be added to calculate the total static height accurately.

Definition of Hydrostatic Pressure (HSP) & Bottom Hole Pressure (BHP)

Hydrostatic pressure is defined as the pressure at the bottom of a well exerted by the weight of the column of water (or other fluid in the well) and is a function of the vertical height of the water column.

In a typical water well, bottom hole pressure (BHP) is identical to HSP and is the pressure exerted by water as measured at the bottom of the well.

HSP will be greater than the pressure exerted by the column of water at the point of water entry into the well piping at a foot valve or into the well pump at a submersible pump because those pick-up points are normally kept several feet above the actual well bottom.

 

Definition of Total Dynamic Head (TDH)

Really? As used by well drillers in describing well properties and in many textbooks cited in this article series, static head is used as we have defined it here.

Alternatively, in hydraulics, static head is sometimes used as a synonym for pressure head - the water pressure measured at the bottom of a column of water.

Static head in this use could for clarity be called pressure head, or static head pressure.

In fluid dynamics, Total Dynamic Head (TDH) is the total equivalent height that a fluid is to be pumped, taking into account friction losses in the pipe. TDH = Static Height + Static Lift + Friction Loss. Also written as

h_total = P2 - P1 / pg

Where

h_total is the total equivalent height that a fluid has to be lifted or pumped including taking into account the friction losses in the pipe.

TDH is a measure of the amount of work that the pump must perform per unit of weight per unit volume of liquid. - Wikipedia https://en.m.wikipedia.org/wiki/Total_dynamic_head

Relation of TDH to Well Flow Rate

We will also have to include the rate at which water runs in to the well while we're pumping water out.

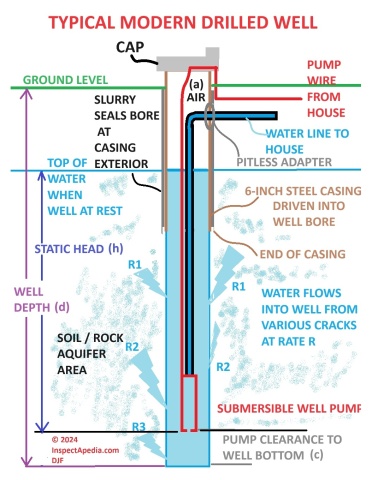Looking at our well sketch and repeated at Components of a Drilled Well with a Submersible Water Pump described

at SUBMERSIBLE WELL PUMPS, and just considering the vertical arrows at the left side, we see that we have

• total well depth (d), which in more detail is comprised of
• the air gap at the top of the well (a),
• the pump clearance at the bottom of the well (c), and
• the static head (h) which is the height of the column of water inside the casing which can be pumped out by the water pump when it operates.

 

Definition of Static Lift or Suction Head

For completeness and of more interest to hydraulics engineers and well drillers is static lift.

Static lift is defined as the height that water must rise before arriving at the pump inlet.

Static lift in a well is the height of water in the well bore from the bottom of the well up to the point of water entry into the foot valve or into the submersible pump inlet.

Definition of Head Loss or Friction Loss

Head loss or friction loss is defined as the energy consumed by turbulence or friction inside the well casing and well piping during pumping.

Head loss in a well water system is a function of water pipe length, diameter, bends or elbows, fittings (whose edges form obstructions to water flow inside the pipe), and even piping material.

If your well piping contains many bends and fittings, the effect is either more energy consumption to move water through the system or reduced water flow rate.

How to Calculate the Water Volume in a Water Well

can now be found

at WELL WATER VOLUME CALCULATION

 

Does the Static Head Quantity in a Well Change?

Absolutely. The static head, the amount of water in a well when the well is "at rest" - that is, no one has pumped water out of the well for some time and the well has filled back up as much as it's going to - changes:

• The well's static head will usually be at its lowest during the dry season of the year
• The water well's static head will usually be at its highest during the wettest season of the year, or after a period of heavy rainfall or heavy snow melt
• A well's static head may drop precipitously in response to events that disturb the soil or water bearing rock nearby, such as road or foundation blasting
• A well's static head may drop precipitously or even disappear entirely - leaving the well "dry" in response to changes in the underlying rock strata or on occasion if someone drills another water well nearby, tapping the same aquifer.

 

Research on Total Dynamic Head

1. Wikipedia, "Total dynamic head", retrieved 2021/02/05 original source: https://en.wikipedia.org/wiki/Total_dynamic_head
2. Wikipedia, "Hydraulic head", retrieved 2021/02/05 original source: https://en.wikipedia.org/wiki/Hydraulic_head
3. WolflramAlpha, Total Dynamic Head Calculator: https://www.wolframalpha.com/input/?i=total+dynamic+head
4. March Pump, "How to Calculate Total Dynamic Head for an Industrial Pump" retrieved 2021/02./05 original source: https://www.marchpump.com/blog/how-to-calculate-total-dynamic-head-for-industrial-pump/#:~:text=15%20feet%20of%20vertical%20distance,feet%20of%20total%20dynamic%20head.
5. Hunter Industries, PIPE FRICTION LOSS TABLES [PDF] Hunter Residential & Commercial Irrigation,
   
   AUSTRALIA: Hunter Industries, Suite 7, 202 Ferntree Gully Road Notting Hill, Melbourne VIC 3168
   CHINA B1618, Huibin Office Bldg. No.8, Beichen Dong Street Beijing 100101 China
   
   EUROPE Avenida Diagonal 523, 5o-2a Edificio Atalaya 08029 Barcelona, SPAIN
   MEXICO Calle Nordika #8615 Colonia la Joya Tijuana, B.C., Mexico CP 22640
   MIDDLE EAST P.O. Box 2370 Amman,11941, Jordan
   
   " USA - Headquarters: Hunter Industries, 1940 Diamond Street San Marcos, CA 92078 USA,
   retrieved 2021/02/05, original source: https://www.hunterindustries.com/sites/default/files/tech_friction_loss_charts.pdf
   Excerpts [minor editing by InspectApedia]:
   
   STATIC PRESSURE: One foot of elevation change results in a change in static pressure of .433 psi.
   
   5 FACTORS in CALCULATING DYNAMIC PRESSURE in a piping system (when water is flowing) varies according to these following five factors, but is always less than static pressure for that same point.
   
   1. Velocity (of water–normally measured in feet per second)
   2. Inside Diameter (of pipe)
   3. Roughness (of inside wall of pipe)
   4. Length (of pipe)
   5. Change in Direction (such as elbows and tees)
   
   NOTE: This does not include remote control valves, backflow prevention devices, etc. The manufacturers' performance charts must be consulted for pressure loss information.
6. Pipe flow friction loss calculator, at http://www.freecalc.com/fricfram.htm
7. Washington State University, Total Dynamic Head Calculator, WSU Extension, "Irrigation in the Pacific Northwest", Prosser - IAREC, 24106 N Bunn Rd, Prosser WA 99350-8694, 509-786-2226, resource provided jointly to include Oregon State Univeristy Extension & University of Idaho Extension, retrieved 2021/02/05, original source: http://irrigation.wsu.edu/Content/Calculators/General/Total-Dynamic-Head.php
   Excerpt:
   
   "Head" is a word engineers use for pressure. This calculator determines the pressure (head) required just after the pump, and the pressure (head) that the pump must generate or add.
   
   The required pressure just after the pump (total dynamic head) includes pre-existing pressure of water entering the pump, pressure needed to overcome elevation differences (sometimes pressure is added if flowing downhill), and the pressure losses due to friction in the pipes in order to produce the required pressure at the emitters, or sprinklers.

...

---

---

ADVERTISEMENT

---

---

Reader Q&A - also see RECOMMENDED ARTICLES & FAQs

On 2021-01-26 by Y. P. Sundriyal - the static head is the actual height of the water column

if we have water level and depth of well can we calculate initial head?

On 2021-01-27 by (mod)

Exactly right, YP the static head is the actual height of the water column in the well when the well is at rest and has fully recovered from any recent use.

Height and bore diameter allow calculation of the static head in gallons or liters.

We give those details above on this page.

On 2021-01-05 by Jerry Steele

Thanks for the fast reply! Nice website by the way.

When measuring current draw of a well pump is it reasonable to assume that it is proportional to TDH, which is a measure of the amount of work that the pump must perform?

On 2021-01-05 by (mod) - variations in current drawn by a water pump

Jerry

The current draw of a water pump will indeed be (perhaps only slightly) reduced in certain circumstances such as

When the pump's inlet or outlet pressure is restricted - lower pressure = less work = less current draw.

But

Watch out: as Terry Love points out, if you use a variable speed pump and you slow the pump speed you will actually use more total energy per gallon of water pumped.

Reference:

Terry Love, "Variable speed pumps and energy uses" - original source: https://terrylove.com/forums/index.php?threads/variable-speed-flow-pumps-and-energy-usage.35009/
Excerpt:
Example;
1 HP pump at full speed puts out 10 GPM and pulls a full 1 HP load, which is 10 gallons per horse power.

When slowing down the RPM, the amps will drop by 50%. This is why so many people think, and can make you believe, they are saving energy. However, when slowed to 50% load, the pump is only moving 1 GPM, and using ½ HP load. That is only 2 gallons per horse power, or 500% more energy used when varying the speed of the pump.

So there is NO return on investment.

Really? Some readers reported making actual current draw (Amps) measurements using a variable speed pump and observing that the actual current draw at reduced output is only very slightly-reduced.

The current draw variation is absolutely bound to be quite different among water pump brands, models, and pump tpes.

VFD (Variable Frequency Drive) pumps may actually use more electrical energy per gallon when running at slower rates.

See

• WATER PUMP VARIABLE FREQUENCY / VARIABLE SPEED DRIVE (VFDs)

Also see

• CSIDesigns, HOW TO READ A PUMP CURVE, pump curve, pump calculator, centrifugal pump, positive displacment pump, Central States Industrial Headquarters 2700 N Partnership Blvd Springfield, MO 65803-8208 USA, Tel: 800 654 5635, retrieved 2021/02/05, at https://www.csidesigns.com/blog/articles/how-to-read-a-pump-curve

...

Continue reading at WELL YIELD, SAFE LIMITS or select a topic from the closely-related articles below, or see the complete ARTICLE INDEX.

Or see WELL DYNAMIC HEAD & STATIC HEAD DEFINITION FAQs - questions & answers posted originally on this page.

Or see these

Recommended Articles

• WELL CASING DIAMETER CHOICE
• WELL CHLORINATION SHOCKING PROCEDURE if you need to disinfect a well
• WELL CHLORINATION DRIVEN SAND POINT
• WELL FLOW RATE
  • WELL DYNAMIC HEAD & STATIC HEAD DEFINITION
  • TOTAL DYNAMIC HEAD DEFINITION
  • WELL WATER VOLUME CALCULATION
  • WELL YIELD, SAFE LIMITS
  • WELL YIELD DEFINITION
  • WELL YIELD IMPROVEMENT
• WELL FLOW TEST for WATER QUANTITY

Suggested citation for this web page

WELL DYNAMIC HEAD & STATIC HEAD DEFINITION at InspectApedia.com - online encyclopedia of building & environmental inspection, testing, diagnosis, repair, & problem prevention advice.

Or see this

INDEX to RELATED ARTICLES: ARTICLE INDEX to WATER SUPPLY, PUMPS TANKS WELLS

Or use the SEARCH BOX found below to Ask a Question or Search InspectApedia

Ask a Question or Search InspectApedia

Questions & answers or comments about water well flow rate, well recovery rate, and well water quantity - does your well run out of water?.

Try the search box just below, or if you prefer, post a question or comment in the Comments box below and we will respond promptly.

Note: appearance of your Comment below may be delayed: if your comment contains an image, photograph, web link, or text that looks to the software as if it might be a web link, your posting will appear after it has been approved by a moderator. Apologies for the delay.

Only one image can be added per comment but you can post as many comments, and therefore images, as you like.
You will not receive a notification when a response to your question has been posted.
Please bookmark this page to make it easy for you to check back for our response.
Our Comment Box is provided by Countable Web Productions countable.ca

Citations & References

In addition to any citations in the article above, a full list is available on request.

---

ADVERTISEMENT

---