How to calculate the diameter of a saw blade from measuring the marks it left on wood, using the Intersecting Chord Theorem ICT. This lets us calculate the diameter of a circle given a few simple measurements.

This article series describes simple calculations that let us find the size of the circular saw blade that left rounded saw blade marks or "arcs" on a section of wood or other material.

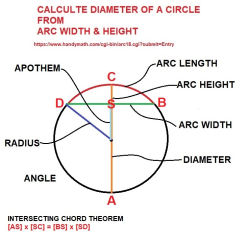
How Calculate the Diameter of a Circle (like a saw blade) using the Intersecting Chord Theorem

By examining curved saw marks in wood boards or beams we can calculate the size of the saw blade that left those marks. Knowing the size of the blade may help us guess at the age of the wood, or at least when it was milled.

If you know the width of the saw blade mark arc and arc height you can easily compute the diameter of the circular saw blade that milled that wooden board or beam.

We explain that here using a method called the intersecting chord theorem.

Our photo above shows a 44-inch diameter saw blade dating from the early 1900s.

[Click to enlarge any image]

This 44-inch diameter blade will have a circumference (the distance around its outer edge) of about 138 inches.

If on an old board or timber we found saw cut marks made by this saw blade, when we put our ruler down 1.5" from the arc of one of those marks and draw a line straight across between the two edges of the arc (the horizontal green line in our photo), at the middle of that line and at right angles to it would be a longer line that crosses the origin of the circle of the saw blade (the vertical hellow, gray and red line in our photo.

On a 14" circular saw blade, an arc heightH of 1.5" would find an arc width W of about 16".

How on earth do we know that? Simple arithmetic.

Despite all of my marks and names and lines on the saw blade shown here, the math is actually quite easy.

Use the Intersecting Chord Theory to Calculate the the Diameter of a Circular Saw Blade from its Arc Marks

It is possible to calculate the saw blade diameter from a few simple measurements using simple algebra.

Some carpenters and wood or old house researchers remember their algebra class. I do. Thank you Mrs. Revere.

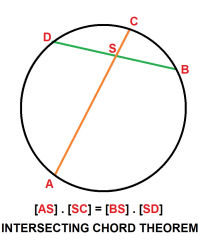
The Intersecting Chords Theorem ICT

When two chords intersect each other inside a circle, the products of their segments are equal.

That theorem says that if you let two straight lines across any part of a circle intersect one another so that each line is divided into two parts, the product of the two parts of one line will be the same as the product of the other two parts of the other line.

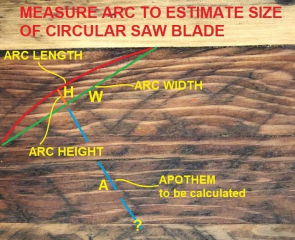
We want to know the diameter or "size" of the circular saw blade that left the saw marks on the wood in our photo given below.

Our photo below uses an actual arc or curved line left in lumber found in a San Francisco CA home reported to have built in the 1920s. The these marks are described further

at SAW & AXE CUTS, TOOL MARKS, AGE

Looking at the circular saw kerf marks in the photo, we will use two numbers that are easy to measure - the orange arc height H and the green arc width W marked on the photo to obtain the diameter D of the circular saw blade.

Let's map the intersecting chord theorem onto the actual circular saw kerf mark on an old bit of wood - shown in our photo above.

Calculate the Circle (or saw blade) Diameter using the Intersecting Chord Theorem

First let's look more closely at the intersecting chord theorem for the case in which one of the c

Using the illustration above, and adapting comments from 1728.org cited below, we start with the intersecting chord theorem:

Whenever 2 chords (in the case above, AB and CD) of a circle intersect at a point E, then AE • EB = CE • ED

Notice that CD is giving us the diameter of the circle, which is what we seek when we want to estimate the size of a circular saw blade from the arced curve saw blade mark it leaves in lumber.

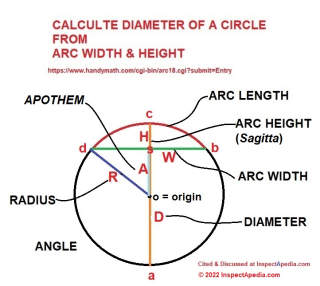
We measured our chord width W as 2" and our arc height H as 0.125"

Our special case of seeking an apothem for a chord that passes through the center of a circle should be calculated as

1/2W x 1/2 W = H x (D - H)

where

W is the chord width that we measure.

H is the arc height that we measure

D is the diameter of the circle (or saw blade)

and then where, when using the intersecting chord theory, now having three numbers out of the four in the ICT, we can solve for the Diameter (we don't need the Apothem).

Plugging our measurements, we will split W in half to prepare to use the intersecting cord theorem formula which, for our drawing above, states

ds x sb = cs x sa

where W = 2 and ds and sb that make up the full length of W are each = 1/2 W or 1

[Note: To use the ICT formula we can simply split W in half - because in this case the vertical Diameter line (illustrated above) bi-sects (cuts in half) our W line.]

where H or the Sagitta = 0.125 = cs

Where D is the diameter that we want to calculate:

1 x 1 = 0.125 x D

1 = 0.125A

1 / 0.125 = A

D = 8

This method says those saw blade marks or saw-kerf-marks tell us that the saw blade diameter is eight inches.

General Case vs. Special Case of the Intersecting Chord Theorem

...

Above, thanks to our contributor Al Carson, we show both our special case (using the origin of the circle) and the more-general case of the intersecting chord theorem.

Notice that in the more-general case the longer chord does not have to pass through the origin of the circle.

A circle chord is a line segment whose endpoints lie on the circle. The sagitta is the distance from the center of the arc bridged by the chord to the center of the chord. The apothem is the distance from the center of the chord to the center of the circle.

A nice introduction to the intersecting chord theorem is at https://www.mathopenref.com/chordsintersecting.html

The general intersecting chord theorem tells us that the chord segments

[AS] x [SC] = [BS] x [SD]

no matter where the chords are drawn across a circle

The special case of the intersecting cord theorem that we used here takes advantage of knowing that the full chord AC passes through the origin of the circle.

Contributors

Special thanks to Al Carson for technical assistance, review, and for pointing out that my original algebraic calculations were incorrect and that normal people would prefer to use an apothem calculator or arc calculator like that we cite here.

• Carson, Dunlop & Associates Ltd., 120 Carlton Street Suite 407, Toronto ON M5A 4K2. (416) 964-9415 1-800-268-7070 info@carsondunlop.com. The firm provides professional HOME INSPECTION SERVICES,        HOME INSPECTION TRAINING,        Horizon INSPECTION SOFTWARE    &    PUBLICATIONS. Alan Carson is a past president of ASHI, the American Society of Home Inspectors. Thanks to Alan Carson and Bob Dunlop, for permission for InspectAPedia to use text excerpts from The Home Reference Book & illustrations from The Illustrated Home.
  
  Alan Carson is a frequent contributor of technical content and technical review of articles at InspectApedia.com
• Calculator City, CIRCLE FORMULAS [PDF] 1728 Software Systems, - retrieved 2022/11/13 original source: https://www.1728.org/circpart.htm
• Math Open Reference, Intersecting chord theorem, 2021/08/20 https://www.mathopenref.com/chordsintersecting.html
• Math Open References, Sagitta, the height of an arc or segment. 2022/02/05 original source: https://www.mathopenref.com/sagitta.html
  
  Sagitta length s = r ± √( r² − l² ) where r is the radius of the arc (or circle from which the arc is cut) and l is 1/2 of the arc chord length (the distance across the base of the arc).
  
  This source points out an alternative way to find the diameter of our circular saw blade: if we know the sagitta (arc height in our discussion above on this page) and the arc width l, (the length of the chord drawn across the bottom points of the arc, then we can find the radius r of the circle from which the arc was snipped (our partial circular saw kerf mark) and of course 2r = d, the diameter of the circle (or our circular saw blade):
  
  r = s² + l² / 2 s
• Stack Exchange: The algebraic proof for the formulas used above to compute the diameter of our circular saw from its arc width and height is at Mathematics on the Stack Exchange at
  - https://math.stackexchange.com/questions/564058/calculate-the-radius-of-a-circle-given-the-chord-length-and-height-of-a-segment
  
  Alternatives for calculating the diameter of a circle when given the height and width of an arc using math or using trigonometry
  

...

Continue reading at SAW & AXE CUTS, TOOL MARKS, AGE, or select a topic from the closely-related articles below, or see the complete ARTICLE INDEX.

Or see these

Recommended Articles

• AGE of a BUILDING, HOW to DETERMINE - home
• ARCHITECTURE & BUILDING COMPONENT ID
• FRAMING AGE, SIZE, SPACING, TYPES
• FRAMING MATERIALS, AGE, TYPES
• FRAMING METHODS, AGE, TYPES
• KIT HOMES, Aladdin, Sears, Wards, Others
• LOG HOME CONSTRUCTION
• MODULAR CONSTRUCTION
• NAILS, AGE & HISTORY
• PANELIZED CONSTRUCTION
• PRE-CUT LUMBER CONSTRUCTION & LEAVITTOWN
• SAW & AXE CUTS, TOOL MARKS, AGE
• SAW BLADE SIZE CALCULATED from SAW MARKS
• SAW BLADE MARKS to SAW SIZE CALCULATION ICT

Suggested citation for this web page

SAW BLADE MARKS to SAW SIZE CALCULATION ICT at InspectApedia.com - online encyclopedia of building & environmental inspection, testing, diagnosis, repair, & problem prevention advice.

Or see this

INDEX to RELATED ARTICLES: ARTICLE INDEX to BUILDING AGE

Or use the SEARCH BOX found below to Ask a Question or Search InspectApedia

Ask a Question or Search InspectApedia

Try the search box just below, or if you prefer, post a question or comment in the Comments box below and we will respond promptly.

Note: appearance of your Comment below may be delayed: if your comment contains an image, photograph, web link, or text that looks to the software as if it might be a web link, your posting will appear after it has been approved by a moderator. Apologies for the delay.

Only one image can be added per comment but you can post as many comments, and therefore images, as you like.
You will not receive a notification when a response to your question has been posted.
Please bookmark this page to make it easy for you to check back for our response.
Our Comment Box is provided by Countable Web Productions countable.ca

Citations & References

In addition to any citations in the article above, a full list is available on request.

---

ADVERTISEMENT

---